密码学基础

密码学概述

• 密码：认证以及 保证通信信息的完整性、机密性

• 认证： 便于授权以及管理

• 机密性：为了防止信息被窃听，因此需要对信息进行加密，对应的密码技术主要就是对称加密和非对称加密。

• 完整性：为了防止信息被篡改，因此需要对信息进行完整性校验，对应的密码技术有单向散列函数、消息认证码、数字签名。

• 不可否认性：为了防止发送者发布信息后否认自己发布过，因此需要证据来证明信息是否由发送者发布，对应的密码技术为数字签名。

• 过程：

  

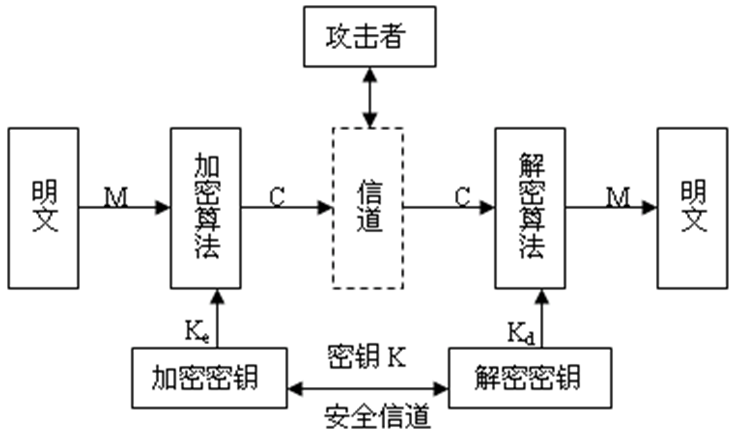
主要思想

分组密码：

设M为明文，分组密码将M划分为一系列明文块Mi，通常每块包含若干字符，并且对每一块Mi都用同一个密钥Ke进行加密。M=(M1,M2,…,Mn) ，C=(C1,C2 ,…,Cn,)，其中Ci=E(Mi,Ke)，i=1,2…,n。如：DES、AESd

序列密码：

将明文和密钥都划分为位(bit)或字符的序列，并且对明文序列中的每一位或字符都用密钥序列中对应的分量来加密。M=(M1,M2,…,Mn) ，Ke=(ke1,ke2,…,ken)，C=(C1,C2,…,Cn)，其中Ci=E(mi,kei)，i=1,2,…,n。

如：RC4

古典密码

单表替换密码

• 加密：将单表替换加密也是逐个字母地加密明文。在加密时，将会按照某种无序的对应规则，并按照这个规则将明文每个字母替换而得到密文。
• 解密：明文和密文没有明显联系，需要两个人都拿都表来对照。
• 较短的密码可以观察之后直接爆破，较长的密码可以进行频率分析。

凯撒密码

• 又称移位密码
• 就是将26个字母简单的移动位置

abcdefghijklmnopqrstuvwxyz
-->右移动两个位：
yzabcdefghijklmnopqrstuvwx
.....其他类似

• 加密结果只有26种，所以可以直接爆破(用python自己写脚本)
• 网上有很多在线解密网站，比如：http://ctf.ssleye.com/（但这个网站有的需要收费）

多表代换密码

加密后字母不再保持原来的频率。

base64

• base64编码，在CTF 中比较常见，base64编码后的字符串的长度一定会被4整除，包括用作后缀的等号吧；如果明文字符数不能被3整除，余1时，1个字符转为2个，补2个等号，共4个字符；余2时，2个字符转为3个字符，补1个等号，共4个字符

• base64不仅可以编码字符串，也可以编码图片，

• 严格来说base64不能算是一种加密，只能说是编码转换，跟ASCII码与Unicode编码一样

• http://imgbase64.duoshitong.com

• 栗子：

  RkxBR3tCSTdfMVNDXzZhYn0=

其他常用古典密码

这个具体就自己搜搜呗

• 栅栏密码
• 培根密码
• 键盘密码
• 猪圈密码

。。。。。。

现代密码学

简介

• 对称加密

  只有一个密钥，加密和解密使用相同的密钥。需要双方协商密钥易泄露，密钥数量大难以管理

• 非对称加密

  一般有公钥(public key)与私钥(private key)。A生成一对密钥，把公钥向其他人公开，自己保留私钥。得到公钥的B把信息加密后发给A，A再用自己的私钥进行解密

• 现代加密策略

  一般先使用非对称加密的方式将对称加密所需的密钥进行加密交换，之后的通信可以通过对称加密进行，结合了二者的优点

RSA

RSA-数论基础

• 互质

  如果两个正整数，除了1以外，没有其他公因子，我们就称这两个数是互质关系

• 欧拉函数

  小于等于n的正整数中与与n构成互质关系的个数。对于素数p, φ(p)=p-1，对于对两
  个互质的数p,q， φ(pq)=φ(p)φ(q) = (p-1)(q-1)

• 模反元素

  ab ≡ 1 (mod r), 则a,b互为模r的模反元素

• 贝祖等式

  若设a,b是整数，则存在整数x,y，使得ax+by=gcd(a,b)

• 定理 ： 如果两个正整数a和n互质，那么一定可以找到整数b，使得ab-1被n整除，或者说ab被n除的余数是1

• 取模运算与同余的概念

  如果存在一个正整数m与两个整数a,b，如果a-b能够被m整除，也就是说m|(a-b),那么a和b模m同余。记为：

  $$a \equiv b \quad mod(m)$$

• 模指数运算

  模指数运算即先进行指数运算，之后再进行取模运算。

  $$a \equiv b^c \quad mod(m)$$

  #python代码
  pow(b,c,m)

• 扩展欧几里得(egcd)

  已知a, b求解一组x，y，使它们满足ax+by = gcd(a, b)，这是一个递归的实现方式

  简单的证明过程:

  设a>b

  1. 当b = 0时，gcd(a,b) = a

     此时 x = 1 , y = 0

  2. 当b>0时

     由贝祖等式可知：

     ​ 对于a,b的解为x1,y1，我们有：

     $$a*x_1 + b*y_1 = gcd(a,b)$$

     ​ 对于b,a%b的解为x2，y2，我们有：

     $$b*x_2 + (a\%b)*y_2 = gcd(b,a\%b)$$

     由欧几里得算法可知：

     $$gcd(a,b) = gcd(b,a\%b)$$

     所以：

     $$a*x_1 + b*y_1 = b*x_2 + (a\%b)*y_2$$

     又：

     $$a\%b =a-\lfloor \frac{a}{b}\rfloor*b$$

     故：

     $$a*x_1 + b*y_1 = b*x_2 + (a-\lfloor \frac{a}{b} \rfloor*b)*y_2 \\ a*x_1 + b*y_1 = a*y_2 + (x_2-\lfloor \frac{a}{b} \rfloor*y_2)*b$$

     所以：

     $$\begin{array}{*{20}{l}} { \left\{ \begin{array}{*{20}{c}} {x_1 = y_2 }\\ {y_1 = x_2-\lfloor \frac{a}{b} \rfloor*y_2 }\\ \end{array}\right. }\\ \end{array}$$

     进行递归求解，最终可以得到x1，y1,扩展欧几里得算法一般用来求模逆，如求解

     $$28^{-1}mod75$$

     最终的结果是:

     $$3*75-8*28=1$$

     所以此时x1=3,y1=-8但在模75范围内，y1=75-8=67

     后续利用扩展欧几里得和下列公式求解d。

     $$e*d \equiv = 1 mod(\varphi(n))$$

  #python实现代码：
  def extendedGCD(a, b):
      #a*xi + b*yi = ri
      if b == 0:
          return (1, 0, a)
      #a*x1 + b*y1 = a
      x1 = 1
      y1 = 0
      #a*x2 + b*y2 = b
      x2 = 0
      y2 = 1
      while b != 0:
          q = a / b
          #ri = r(i-2) % r(i-1)
          r = a % b
          a = b
          b = r
          #xi = x(i-2) - q*x(i-1)
          x = x1 - q*x2
          x1 = x2
          x2 = x
          #yi = y(i-2) - q*y(i-1)
          y = y1 - q*y2
          y1 = y2
          y2 = y
      return(x1, y1, a)

RSA加密解密原理

常见变量含义

n: 大整数，我们称之为模数(modulus)

p,q:大整数的两个素因数(factor),n = p*q

e,d:互为模反的两个数，其中{e,n}构成公钥，{d,n}构成私钥

c,m:c = pow(m, e, N)，得到的c即为密文,m = pow(c, d, N)，得到的m即为明文

生成密钥

1. 选择两个大素数p和q，n = p*q

2. 选择一个整数e，满足条件

   $$1 < e < \varphi(n)\\ gcd(e,\varphi(n)) = 1$$

3. 其中{e,n}是公钥，{d,n}是私钥

RSA安全性保障

1. e的选择不可以太小，否则可能会被爆破

2. p和q的差值尽可能大一点

3. d的选择不能太小，也不能太大，一般满足

   $$d\ge n^{\frac{1}{4}}$$

基本的攻击方法

基本题型

变种RSA

Rabin算法

e = 2，与RSA类似但这个函数不是单射，一个密文能解出4个明文

1. 取两个大素数p与q，使得p≡q≡3(mod 4)(保证为奇素数)

2. 加密：

   $$c=m^2 \quad mod( n)$$

3. 解密：

   $$m^2≡c \quad mod( n)$$

理论基础：

• 二次剩余

  $$对于式子y^2 = a \quad mod \quad p,称a是y模p的二次剩余$$

• Euler准则

  设p为一个奇素数，a是一个正整数。那么a是一个模p二次剩余当且仅当

  $$a^{\frac{p-1}{2}} \equiv 1\ (mod\ p)$$

  证明：

  1. 充分性

  $$假定a\equiv y^2\ (mod\ p)。由欧拉定理可知（p为素数）a^{p-1} \equiv 1(mod\ p) \\ 对于任一a \ne 0 (mod\ p)成立，所以\qquad\qquad\qquad\qquad\qquad\qquad\qquad\\ a^{\frac{p-1}{2}} \equiv (y^2)^{\frac{p-1}{2}}(mod\ p)\quad \\ \equiv y^{p-1}(mod\ p) \\ \equiv 1(mod\ p) \quad \$$

  1. 必要性

  $$假定a^{\frac{p-1}{2}}\equiv1(mod\ p)。设b是一个模p的元素。那么a\equiv b^i(mod\ p)对于\\ 某个整数i，我们有\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\ \ \\ a^{\frac{p-1}{2}}\equiv(b^i)^{\frac{p-1}{2}}(mod\ p) \quad \quad\\ \equiv b^{i(\frac{p-1}{2})}(mod\ p) \\ 由欧拉定理可知，此时i应该为偶数，所以a的平方根为\pm b^{\frac{i}{2}}(mod\ p )\quad\ \$$

• p,q要求

  $$当p \equiv 3\ (mod\ 4)时，有以下公式：\qquad\qquad \qquad\qquad\quad \qquad\qquad\quad \qquad\qquad\quad \qquad\qquad\quad\\ (\pm \ y^{\frac{p+1}{4}})^2 \equiv y^{\frac{p+1}{2}}(mod\ p) \qquad\qquad\quad \quad \\ \equiv y^{\frac{p-1}{2}}*y(mod\ p) \ \\ \equiv y(mod\ p) \qquad \ \ \ \$$

• 中国剩余定理

  用于求解同余方程组

解密

$$y模p的两个平方根为\pm y^{\frac{p+1}{4}}(mod\ p) \\ y模q的两个平方根为\pm y^{\frac{q+1}{4}}(mod\ q)$$

由欧拉公式可求解p关于q的模逆以及q关于p的模逆：

$$y_p * p+y_q*q = 1$$

由中国剩余定理可知：

$$r = (yp * p * mq + yq * q * mp)\ mod\ n \\ -r = n - r \qquad \qquad \qquad \qquad \qquad \qquad\\ s = (yp * p * mq - yq * q * mp)\ mod\ n \\ -s = n - s \qquad \qquad \qquad \qquad \qquad \qquad \\$$

#python实现脚本
#参数待定
def rabin_decrypt(c, p, q, e=2): 
    n = p * q 
    mp = pow(c, (p + 1) / 4, p) #整除 ⽤// 
    mq = pow(c, (q + 1) / 4, q) 
    yp = gmpy2.invert(p, q) 
    yq = gmpy2.invert(q, p) 
    r = (yp * p * mq + yq * q * mp) % n 
    rr = n - r 
    s = (yp * p * mq - yq * q * mp) % n 
    ss = n - s 
    return (r, rr, s, ss)

三素数RSA

1. 取三个素数p,q,r
2. 计算n=p*q*r
3. 计算欧拉函数

$$\varphi{n} = (p-1)*(q-1)*(r-1)$$

1. 选择一个e值，满足：

$$1 < e < \varphi(n)\\ gcd(e,\varphi(n)) = 1$$

1. 计算d值， $$e*d \equiv 1 \quad mod(\varphi(n))$$

正确性证明

椭圆曲线

椭圆曲线加密算法，即：Elliptic Curve Cryptography，简称ECC，是基于椭圆曲线数学理论实现的一种非对称加密算法。相比RSA，ECC优势是可以使用更短的密钥，来实现与RSA相当或更高的安全。据研究，160位ECC加密安全性相当于1024位RSA加密，210位ECC加密安全性相当于2048位RSA加密。

• 椭圆曲线的一般方程为

  $$y^2 = x^3+ax^2+b^2+c$$

• 判别式为

  $$\Delta (E) = -4a^3c+a^2b^2-4b^3-27c^2+18abc \neq 0$$

  比如下面这个图：

  

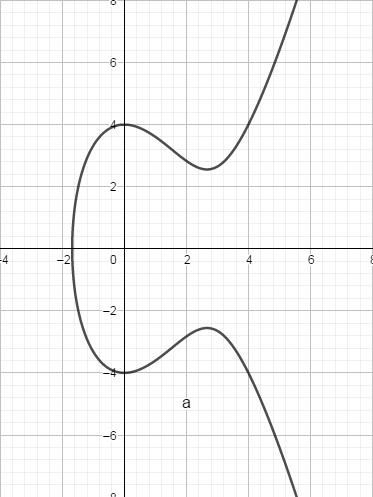
• 密码学中用到的椭圆曲线方程一般限定为

  $$y^2=x^3+ax+b，其中\Delta(E)=4a^3+27b^2 \neq 0$$

定义椭圆曲线的运算规则

• 加法

  过曲线上的两点A、B画一条直线，找到直线与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A+B，即为加法。如下图所示：A + B = C

  

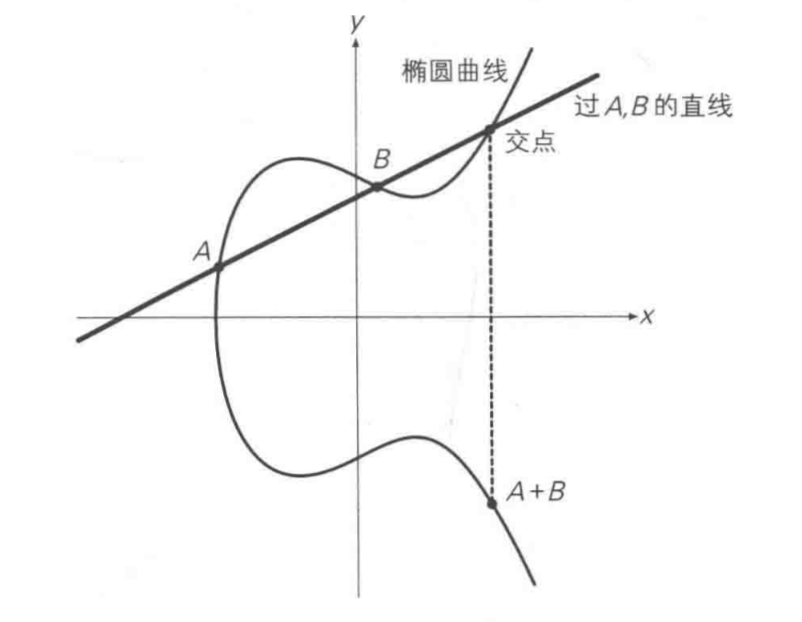
• 二倍运算

  此时上述直线与曲线相切，在这种情况下，将椭圆曲线在A点的切线，与椭圆曲线的交点，交点关于x轴对称位置的点，定义为A + A，即2A，即为二倍运算。

  

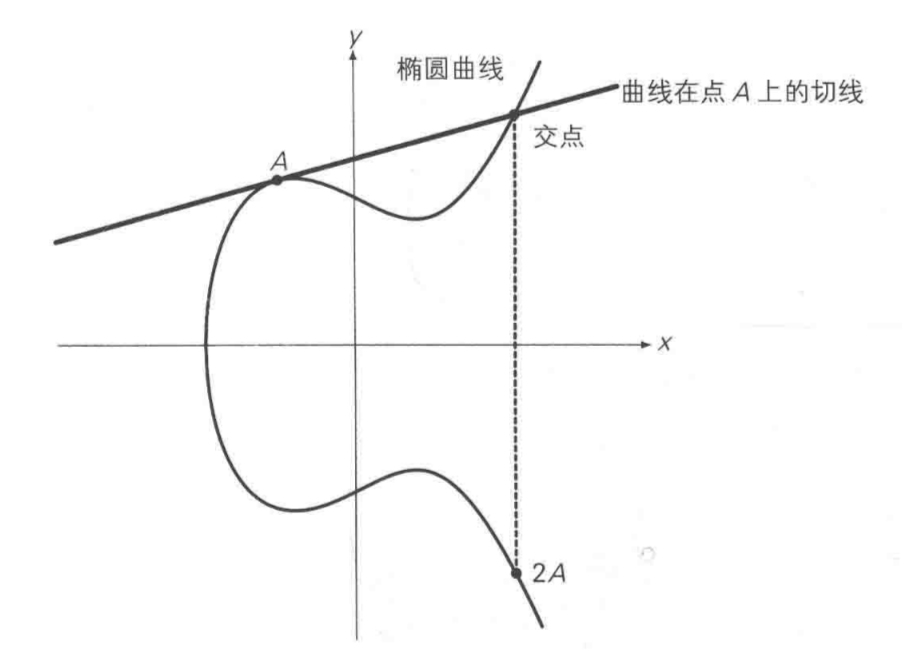
• 正负取反
  A与-A,坐标相当于关于x轴对称

• 无穷远为单位元x

  A+（-A）=O

实数的椭圆曲线

椭圆曲线加密解密原理

由上述所定义的运算，我们知道，当给定一个点G时，已知一个数k求kG并不困难，但是已知kG我们想要求k却是非常困难。
所以我们可以将k当作私钥，K=kG为公钥，

• 加密过程：
  选择一个随机数r，将消息M生成密文C，该密文是一个点对C={rG,M+rK}
• 解密过程：
  M+rK-k(rG)=M

椭圆曲线签名算法原理

• 私钥签名：
  1. 选择一个随机数r，计算点rG，G(x,y)
  2. 根据随机数r、消息M的hash值、私钥k，计算sig = (h+kx)/r (ps:有限域中的除运算都是求逆)
  3. 将消息M、和签名{rG,sig}
• 公钥验证签名：
  1. 接收方收到消息M、以及签名{rG, s}
  2. 根据消息求哈希h
  3. 使用发送方公钥K计算:hG/s+xK/s =rG

为什么需要hash???