RSA-集锦

| | 浏览 次
Words count in article: 7.1k 字 | Reading time ≈ 39 分钟

奇淫技巧

已知dp,dq,c,n,p,q

理论证明

我们知道

所以存在一个值k，使得下式成立

将上述式子分别模p,q，得到

由上述可知，我们可以令

将(5)带入到(4)中，得到

由于gcd(p,q)=1，所以我们得到k值得同余式：

将(7)带入到(5)中，得到

将(8)带入到(1)中，

对于mp以及mq，求法如下：

由费马小定理可知

所以，

这样就万事俱备！！

一般实现代码如下:

1
2
3
4
5
6
7
8
#!usr/env/python3
#coding=utf-8

import gmpy2
mp = pow(c,dp,p)
mq = pow(c,dq,q)
Invq = gmpy2.invert(q,p)
m = (mq+(mp-mq)*Invq*q) % n

已知dp,e,c,n

理论证明

我们可以知道

之后我们可以知道：

将dp*e之后

所以e*dp-1是p-1的k倍，k在（1，e）之中(原因是dp在p-1之内)

下面就就写一下关于爆破e值的脚本,从而求出d

1
2
3
4
5
6
7
8
9
10
11
#!usr/env/python3
#coding:utf-8

import gmpy2
for i in range(e):
    if (e*dp-1)% i == 0:
        if n %(((dp*e-1)//i)+1) == 0:
            p = ((dp*e-1)//i)+1
            q = n//p
            fn = (p-1)*(q-1)
            d = gmpy2.invert(e,fn)

题目

rsa(2019/11/11湖湘杯初赛)

1
2


已知dp,dq

dp = d mod (p-1)

dq = d mod (q-1)

​

已知p+q与pq

根据题目要求可以求出pq与p+q，这时候可以直接求出fn

题目

rsa

Do you know what e is it？

打开文件，有两个文件，一个python文件，一个output

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#output
import gmpy2
from fractions import Fraction
from secret import flag,e
from libnum import *
from os import urandom
k = 1024
p = gmpy2.next_prime(int(urandom(k / 8).encode('hex'),16))
q = gmpy2.next_prime(int(urandom(k / 8).encode('hex'),16))
n = p*q
assert(e<1000)
print n
#自动约分化简
print Fraction(int(p+1),int(p)) +Fraction(int(q+1),int(q))
print pow(123,e,n)
msg = s2n(flag)
assert(msg<n)
print pow(msg,e,n)
1
2
3
4
5
6
#output
9538795663851271297602738029671089878718012242935213096566250130325046936720540247534143498025477544161347330379679111765871420732255741210434736423951962189227302658997497664520929375215715960063615792480965807127438948044298348300153102760490410578638259665656608784635088735809470916136628779400145983632930861883762707606629208260803446083579674497451514650309351925430391515629898218875049677870989016071086844819626778388370764400242376469343158294638240660190754978627356076115228410162956087266527271225439142347304100660800517276772407728290414074912243665126741030948775883739544952378188264714716087909797
19077591327702542595205476059342179757436024485870426193132500260650093873441080495068286996050955088322694660759358223531742841464511482420869472847903924378454605317994995329041858750431431920127231584961931614254877896088596696600306205520980821157276519331313217569270177471618941832273257558800291967266057799408185825199394392306374394195697993019961311696247374832761757990150416392201444079060627610573918631913438062954960835929982836033906925917632413007648356037059843552967726871763559759125837289869091638924336309932526582201350695938677991368335828814565265478203873169858685929462350511138398905572292/
9538795663851271297602738029671089878718012242935213096566250130325046936720540247534143498025477544161347330379679111765871420732255741210434736423951962189227302658997497664520929375215715960063615792480965807127438948044298348300153102760490410578638259665656608784635088735809470916136628779400145983632930861883762707606629208260803446083579674497451514650309351925430391515629898218875049677870989016071086844819626778388370764400242376469343158294638240660190754978627356076115228410162956087266527271225439142347304100660800517276772407728290414074912243665126741030948775883739544952378188264714716087909797
368284101618076523549199130884422355928051525996327977632544904437878504262870825378516827225793010165434494157238379685995430409966951122729243411694569562164062815098110639750101378457641471316188502263725098231679401928494160942213175404259256770984218593245458108598930926260386443799301699336309331946341173652201791293571029025818674575198311845811957606474490230382511996537893448524426809391980637983473305318819523408854264623254226127223862150173575206444726570183096891630129244778802793476295746913846105454198627
7303495910407762399046490836902121070389476875516762048462433039234972742941586801378979220008051262826174054961747648114128456872349675769941760630519744351742977740846748646739901172672743584989842268056810152117350241337045055812845489372389014195433916347255846499434232234822333192328886207187844781726928951986353054876826105507064928478812402103648940709131760865763234071703554208057808885564381400571862422316195578258814602362582573148358552148686182480215663291366798585241933446701357953551496955627421526567152576426417189707335038601040167826900549139608192971559659991213411381604721734898065256138516

分析：利用123对应的那个密文，解出e值，

利用上面的式子，我们可以利用上述的式子

求出p+q后，就可以顺手解出fn

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#!usr/env/python3
#coding=utf-8
#owner: IFpop
#time: 2910/11/2
from z3 import *
import gmpy2
from Crypto.Util import number

n = 9538795663851271297602738029671089878718012242935213096566250130325046936720540247534143498025477544161347330379679111765871420732255741210434736423951962189227302658997497664520929375215715960063615792480965807127438948044298348300153102760490410578638259665656608784635088735809470916136628779400145983632930861883762707606629208260803446083579674497451514650309351925430391515629898218875049677870989016071086844819626778388370764400242376469343158294638240660190754978627356076115228410162956087266527271225439142347304100660800517276772407728290414074912243665126741030948775883739544952378188264714716087909797

sum_pq = 19077591327702542595205476059342179757436024485870426193132500260650093873441080495068286996050955088322694660759358223531742841464511482420869472847903924378454605317994995329041858750431431920127231584961931614254877896088596696600306205520980821157276519331313217569270177471618941832273257558800291967266057799408185825199394392306374394195697993019961311696247374832761757990150416392201444079060627610573918631913438062954960835929982836033906925917632413007648356037059843552967726871763559759125837289869091638924336309932526582201350695938677991368335828814565265478203873169858685929462350511138398905572292
#196075640660409986135975784767502028538644025058282395628670981900974958890619954451344723318649578431744942274184506178219307129498083095220609328355931687266846079805131400737270051437647584592782747418213354229728108610925547647805880482097163218511341484311783416306321402379596024705973981708966729752698
sum_pq = sum_pq-2*n
# c_123 = 368284101618076523549199130884422355928051525996327977632544904437878504262870825378516827225793010165434494157238379685995430409966951122729243411694569562164062815098110639750101378457641471316188502263725098231679401928494160942213175404259256770984218593245458108598930926260386443799301699336309331946341173652201791293571029025818674575198311845811957606474490230382511996537893448524426809391980637983473305318819523408854264623254226127223862150173575206444726570183096891630129244778802793476295746913846105454198627

# for e in range(1000):
#     temp_c = pow(123,e,n)
#     if temp_c == c:
#         print(e)
#         break
# d = (p-1)*(q-1)
e = 251
c = 7303495910407762399046490836902121070389476875516762048462433039234972742941586801378979220008051262826174054961747648114128456872349675769941760630519744351742977740846748646739901172672743584989842268056810152117350241337045055812845489372389014195433916347255846499434232234822333192328886207187844781726928951986353054876826105507064928478812402103648940709131760865763234071703554208057808885564381400571862422316195578258814602362582573148358552148686182480215663291366798585241933446701357953551496955627421526567152576426417189707335038601040167826900549139608192971559659991213411381604721734898065256138516
fn = n-sum_pq+1
d = gmpy2.invert(e,fn)
m = pow(c,d,n)
print(number.long_to_bytes(m))

分解模数N

方法介绍

  • n比较小的话，可以手写脚本进行爆破

    1
    2
    3
    4
    5
    6
    7
    #coding=utf-8

    for i in range(2,n):
        if(n%i == 0):
            p = i
            q = n/i
            break

  • n比较大的话，可以使用一些攻击进行暴力破解，如RSATool或者yafu

  • 一个在线分解大素数的网站：http://factordb.com,这个网站只能分解已经存在分解过的模数n值

题目

xyf(Jarvisoj)

1
2
3
n=3161262255255421133292506694323988711204792818702640666084331634444148712428915950639954540974469931426618702044672318134908678730641981414037034058320359158246813987154679178159391832232990193738454116371045928434239936027006539348488316754611586659587677659791620481200732564068367148541242426533823626586574915275209508300120574819113851895932912208783915652764568319771482309338434364094681579135086703127977870534715039005822312878739611630155714313119545610939253355808742646891815442758660278514976431521933763272615653261044607041876212998883732724662410197038419721773290601109065965674129599626151139566369
e=65537
c=631583911592660652215412683088688785438938386403323323131247534561958531288570612134139288090533619548876156447498627938626419617968918299212863936839701943643735437264304062828205809984533592547599060829451668240569384130130080928292082888526567902695707215660020201392640388518379063244487204881439591813398495285025704285781072987024698133147354238702861803146548057736756003294248791827782280722670457157385205787259979804892966529536902959813675537028879407802365439024711942091123058305460856676910458268097798532901040050506906141547909766093323197363034959926900440420805768716029052885452560625308314284406

使用yafu对模数进行分解：

1
2
p= 56225103425920179745019828423382255030086226600783237398582720244250840205090747144995470046432814267877822949968612053620215667790366338413979256357713975498764498045710766375614107934719809398451422359883451257033337168560937824719275885709824193760523306327217910106187213556299122895037021898556005848927                                             
q = 56225103425920179745019828423382255030086226600783237398582720244250840205090747144995470046432814267877822949968612053620215667790366338413979256357713975498764498045710766375614107934719809398451422359883451257033337168560937824719275885709824193760523306327217910106187213556299122895037021898556005848447

脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#coding=utf-8
#owner:IFpop
#time:2019/10/28

import gmpy2
from Crypto.Util import number

c = 631583911592660652215412683088688785438938386403323323131247534561958531288570612134139288090533619548876156447498627938626419617968918299212863936839701943643735437264304062828205809984533592547599060829451668240569384130130080928292082888526567902695707215660020201392640388518379063244487204881439591813398495285025704285781072987024698133147354238702861803146548057736756003294248791827782280722670457157385205787259979804892966529536902959813675537028879407802365439024711942091123058305460856676910458268097798532901040050506906141547909766093323197363034959926900440420805768716029052885452560625308314284406
n = 3161262255255421133292506694323988711204792818702640666084331634444148712428915950639954540974469931426618702044672318134908678730641981414037034058320359158246813987154679178159391832232990193738454116371045928434239936027006539348488316754611586659587677659791620481200732564068367148541242426533823626586574915275209508300120574819113851895932912208783915652764568319771482309338434364094681579135086703127977870534715039005822312878739611630155714313119545610939253355808742646891815442758660278514976431521933763272615653261044607041876212998883732724662410197038419721773290601109065965674129599626151139566369
e = 65537
p = 56225103425920179745019828423382255030086226600783237398582720244250840205090747144995470046432814267877822949968612053620215667790366338413979256357713975498764498045710766375614107934719809398451422359883451257033337168560937824719275885709824193760523306327217910106187213556299122895037021898556005848927
q = 56225103425920179745019828423382255030086226600783237398582720244250840205090747144995470046432814267877822949968612053620215667790366338413979256357713975498764498045710766375614107934719809398451422359883451257033337168560937824719275885709824193760523306327217910106187213556299122895037021898556005848447
fn = (p-1)*(q-1)
d = gmpy2.invert(e,fn)
m = pow(c,d,n)
print(number.long_to_bytes(m).decode())
#flag{yafu_is_great_2}

Factoring with High Bits Known

当我们知道一个公钥中模数N的一个因子的较高位时，我们就有一定几率来分解N。

需要安装sage

下载好之后，进行如下操作：

1
2
3
4
$ tar xvf sage-8.9-Ubuntu_18.04-x86_64.tar.bz2
$ cd SageMath
$ ./sage  #运行进入交互页面
$ ./sage *.sage   #直接运行程序

模板：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from sage.all import *
import binascii
n = 0x.... # 此处为16进制数
p4 =0x....  #p的高位 16进制
cipher = 0x 密文
e2 = 0xf93b
pbits = 1024
kbits = pbits - p4.nbits()
print p4.nbits()
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
   p = p4+int(roots[0])
   print "p: ", hex(int(p))
   assert n % p == 0
   q = n/int(p)
   print "q: ", hex(int(q))
   print gcd(p,q)
   phin = (p-1)*(q-1)
   print gcd(e2,phin)
   d = inverse_mod(e2,phin)
   flag = pow(cipher,d,n)
   flag = hex(int(flag))[2:-1]
   print binascii.unhexlify(flag)

题目

cry

给了个cry.py文件和访问链接:

nc pwn2.jarvisoj.com 9891

看完代码:

  1. 先随机生成了一个模数n以及e，需要使用n与e对任一一个信息进行加密，然后转成hex形式，传入程序才能走向下一步
  2. 之后给出了使用base64加密的密文，以及使用RSA加密的aes_key和初始向量IV
  3. AES是一种对称加密，也就是加密密钥和解密密钥是相同的
1
2
3
4
5
nc pwn2.jarvisoj.com 9891    
====welcome to cry system====  
give you the public key:                                      n:0x1cf288a5f1759c54d5a2c38e252c14662e5ef2d70294b01e2f08564fc6e6dfad5184972687de2b46102e2e4854191f6d960451e121c8313e9b870d401d49bd90dd9ca8ba6bbfe75c95bbe54b413d5952aec0a97dff2c3f8442cd4c44211d59ec140c3f18712e73f81b5c78a598a42217fb2bba465920b39a9069ab9f0d47d361677c87a82659ac2205aca88c1cb34ffd8d0633f4965f7c9d19fa39fdf5c8b1e4e53aa91e4d82086d090d7fc10393c132e60ec6bbedcb172f41cf84411acaf66003e1d2ee9e69d44f946c805a4c1c69a2d345e2eb379f88f98445ac625ba04ff845fa841de886ccd11219680ffcfd291f43bf07b9455570b4502278a0b0b501db                                                   
e:0x10001     
give me the crypted message in hex:0x115370ba6049a21212d6cd98049f88f881361065a8453796852334c46080867772e450f8a7383c01e79a13a10236f68df473ccf910479df0e0fe507972d04987cc0c755430f2ccaf61a7a13e1cc2e7bbc7aba02efbf5e0c15c931ac11ffc688f24332d3252b077723c4fac1007134f56610ae894552e3fe0207ca3a19d4d2a21a3737882d08d1ac4c4a0524652545bdcc3b102191bfd766e57bd9b4d42987da43ff70466e5cf0fb314f546f4f5774160f6b7eee9650f4d92f4078f6ffe4a16e22f49df6efea9c8dd548233cba2e3ba9251b57b5ef0b6f305bc1721c2fd3361057d95472c4ca2d76a2b284eb78d2884b3584d26b9ee743c35a484c29ff5556fae

通过得到的n,e任一加密一段字符串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#!/usr/bin/python
#coding=utf-8
#owner: IFpop
#time: 2019/10/29

from Crypto.Util import number

m = 'welcome'
m = m.encode('utf-8')

n = 0x190bc1baa378011895e3ca794b1d9918ebd1ffa749f4b0d6495cfafd6c3fd0303b1e9f822478c282c8377c06dabc211f8140bc9696fadb8e7b7bcf145653e4555a2c79b561e613917e5d1f91e439526c4d75b72b34a0827640434cd37004de4b9694407e247d7591b9a7b9067ef53cc4c1087920f057272aaf3c7e23e2ff873e05c383edd23ba87af1acb8d3185636cc265997f8a416e4984b8ede2fa4fa528ba854a1abf8333965289d5b0ff5f44b208905f1a239c83816d67dd689c37b04f954a43984811fe9d9e0e282362a0f3b777f53e26ebf0950bbfcf23d59fc54f52a7473aae116d72ca0fa9a23e779ae47a08af00874f4b5a11fd1dedad8076ea247
e = 0x10001

c = pow(number.bytes_to_long(m),e,n)
print(hex(c))
#0x18f574e08d83e95dec3f1e01ea955d7e9e3eb912fddf3da45ef6173c15872d050f740f4cdd2113c5a20dab2b29bb7f170202340af2bafdd08489c31293a3b556a0d150cbfaff898223c7878f23742898b0a683a0ea9cfdba993fdaa7624caf58c5720cbf08fdeff917d27a3930161fd9f598065a72a88c0b89ed9113f28bb1035f505afff643f93750ed0405dc54edebdc96ab2dfbc0d7360dde1a6b78acd8e9dd781399bfa5209a93ed44571b8a39b02989771baa105253e0c66bedbaa22d8b90318841a85ae82ddab63d93a01c97548681ab96a25f58d0386bedfc2f101a7b42589d661342393513914b8ca1e8d34637f98802d06434fe06d459077fdc8786
#0x5ac23d297db75d07ae452d66ea20870f5ef7a61eb66ec8bfa5e2faa37e4bf45a2fbbf1d0ed0a3be8e9475928491b69c5a143d7da364915a8750db4fb0a69b9d5bdf422c00a6e8da8b352289a9582ab3394e9688166639ed055ca6f8dd68896a7976e285fee56d9d06b44ae82aea182ed12c69a3c8ee9475c52ff8b9458abf93c46a93b34950f61447b3430a6a10313a6f6d3926d33f8f32353ac354a89ab8d03f0aede0f257515208626e61af16a3af2be75ac0dd2d48b3ebada4b7dbab87b89b62d17fc1bff115b0feadf747d9158aab2668e2ef6e37799d00821b42be3a796d218a0b30f157a5ebb83716984e07ae3e7a4ce30553d8d54ae61f5b39078095
#b2fc1f1fa4dda1ecedbcf081013e57d44235ea2b0fd96cf85b09d7e4afba8f920f6b0370fdae1898ab8c887c42fc969265d8dfa1d19a83c900aa77db06791c170dbab565440d9caa0693ccb75954dd30605d5b5642b80812121e

通过交互页面得到密文c以及aes_key和iv，这里只给出p的高位，所以需要我们进行爆破，求出最终的p来，下面是ans.sage文件:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#coding=utf-8
#owner: IFpop
#time: 2019/10/29

import binascii

n = 0x190bc1baa378011895e3ca794b1d9918ebd1ffa749f4b0d6495cfafd6c3fd0303b1e9f822478c282c8377c06dabc211f8140bc9696fadb8e7b7bcf145653e4555a2c79b561e613917e5d1f91e439526c4d75b72b34a0827640434cd37004de4b9694407e247d7591b9a7b9067ef53cc4c1087920f057272aaf3c7e23e2ff873e05c383edd23ba87af1acb8d3185636cc265997f8a416e4984b8ede2fa4fa528ba854a1abf8333965289d5b0ff5f44b208905f1a239c83816d67dd689c37b04f954a43984811fe9d9e0e282362a0f3b777f53e26ebf0950bbfcf23d59fc54f52a7473aae116d72ca0fa9a23e779ae47a08af00874f4b5a11fd1dedad8076ea247
e = 0x10001
p4 =0xb2fc1f1fa4dda1ecedbcf081013e57d44235ea2b0fd96cf85b09d7e4afba8f920f6b0370fdae1898ab8c887c42fc969265d8dfa1d19a83c900aa77db06791c170dbab565440d9caa0693ccb75954dd30605d5b5642b80812121e

c_aes_key = 0x18f574e08d83e95dec3f1e01ea955d7e9e3eb912fddf3da45ef6173c15872d050f740f4cdd2113c5a20dab2b29bb7f170202340af2bafdd08489c31293a3b556a0d150cbfaff898223c7878f23742898b0a683a0ea9cfdba993fdaa7624caf58c5720cbf08fdeff917d27a3930161fd9f598065a72a88c0b89ed9113f28bb1035f505afff643f93750ed0405dc54edebdc96ab2dfbc0d7360dde1a6b78acd8e9dd781399bfa5209a93ed44571b8a39b02989771baa105253e0c66bedbaa22d8b90318841a85ae82ddab63d93a01c97548681ab96a25f58d0386bedfc2f101a7b42589d661342393513914b8ca1e8d34637f98802d06434fe06d459077fdc8786
c_iv =      0x5ac23d297db75d07ae452d66ea20870f5ef7a61eb66ec8bfa5e2faa37e4bf45a2fbbf1d0ed0a3be8e9475928491b69c5a143d7da364915a8750db4fb0a69b9d5bdf422c00a6e8da8b352289a9582ab3394e9688166639ed055ca6f8dd68896a7976e285fee56d9d06b44ae82aea182ed12c69a3c8ee9475c52ff8b9458abf93c46a93b34950f61447b3430a6a10313a6f6d3926d33f8f32353ac354a89ab8d03f0aede0f257515208626e61af16a3af2be75ac0dd2d48b3ebada4b7dbab87b89b62d17fc1bff115b0feadf747d9158aab2668e2ef6e37799d00821b42be3a796d218a0b30f157a5ebb83716984e07ae3e7a4ce30553d8d54ae61f5b39078095
pbits = 1024
kbits = pbits - p4.nbits()
print(p4.nbits())
p4 = p4 << kbits
PR.<x> = PolynomialRing(Zmod(n))
f = x + p4
roots = f.small_roots(X=2^kbits, beta=0.4)
if roots:
   p = p4+int(roots[0])
   print "p: ", hex(int(p))
   assert n % p == 0
   q = n/int(p)
   print "q: ", hex(int(q))
   print gcd(p,q)
   phin = (p-1)*(q-1)
   print(gcd(e,phin))
   d = inverse_mod(e,phin)
   
   m_aes_key = pow(c_aes_key,d,n)
   m_aes_key = hex(int(m_aes_key))
   m_iv = pow(c_iv,d,n)
   m_iv = hex(int(m_iv))

   print("ck:")
   print(m_aes_key)
   print("iv:")
   print(m_iv)
#ck: e014637373b84ef7a9ccefb5b24e097
#iv: 1b892532aabc36ee8975a5793a88fd2f
#这里有一个坑点，就是位数应该和大的那一位是相等的，所以短的那一个应该在前面补0

剩下就可以直接开始解密了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
#coding=utf-8
#owner: IFpop
#time: 2019/10/29

import binascii
from Crypto.Cipher import AES
import base64

flag = 'LEOgtbX8wRuuejn8sBke7yooByv+nDwYTaiINR4GGfY='
key = '0e014637373b84ef7a9ccefb5b24e097'
iv =  '1b892532aabc36ee8975a5793a88fd2f'
cipher = AES.new(key.decode('hex'), AES.MODE_CBC, iv.decode('hex'))
flag = base64.b64decode(flag)
flag = cipher.decrypt(flag)
print(flag)
#aaaaaflag{ok_this_is_a_flag_rsa}

Rabin算法

基本知识

hardRSA——Jarvis OJ

加压后发现两个文件，一个公钥，一个enc文件

使用openssl查看

1
2
3
4
openssl rsa -in pubkey.pem -pubin -text -modulus

#下面是显示
RSA Public-Key: (256 bit)                                                                 Modulus:                                                                                 00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f:                                             1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f:                                             be:30:dd                                                                                 Exponent: 2 (0x2)                                                                         Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD                 writing RSA key                                                                           -----BEGIN PUBLIC KEY-----                                                               MDowDQYJKoZIhvcNAQEBBQADKQAwJgIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr                         yigb/+l/vjDdAgEC                                                                         -----END PUBLIC KEY-----

典型的rabin加密，使用模块叫脚本即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
#coding=utf-8
import string
from Crypto.Util.number import long_to_bytes
import gmpy

def rabin_decrypt(c, p, q, e=2): 
    n = p * q 
    mp = pow(c, (p + 1) / 4, p) #整除 ⽤// 
    mq = pow(c, (q + 1) / 4, q) 
    yp = gmpy.invert(p, q) 
    yq = gmpy.invert(q, p) 
    r = (yp * p * mq + yq * q * mp) % n 
    rr = n - r 
    s = (yp * p * mq - yq * q * mp) % n 
    ss = n - s 
    return (r, rr, s, ss)

with open('flag.enc', 'r') as f:
    c = f.read().encode('hex')
    c = string.atoi(c, base=16)
p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
n = p*q
 
temp = rabin_decrypt(c,p,q,2)
for i in temp:
    print(long_to_bytes(i))
#PCTF{sp3ci4l_rsa}

一句话加密

下载附件得到两个文件，一个图片，一个encode.py

1
2
3
4
#encode.py
c = pow(int(m.encode('hex'), 16),e,n)
c1:62501276588435548378091741866858001847904773180843384150570636252430662080263
c2:72510845991687063707663748783701000040760576923237697638580153046559809128516

e

使用winhex打开查看它，发现末尾有一段

0xc2636ae5c3d8e43ffb97ab09028f1aac6c0bf6cd3d70ebca281bffe97fbe30dd?kobe"

本来以为图片是e.png，所以这是e的值，但发现可以使用yafu将其分解成两个大素数，所以认为这个是模数n

这里还有一个提示信息，就是kobe，图片上的符号表示的是kobecode，还是见识太少

kobe

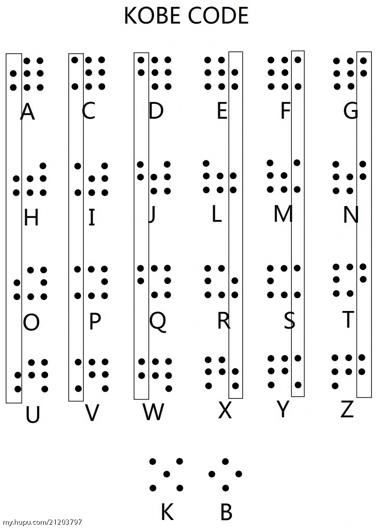
翻译出来是TWO，所以猜测是rabin加密，解密如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#coding=utf-8
#owner: IFpop
#time: 2019/10/15

from Crypto.Util import number
import gmpy2

def rabin_decrypt(c, p, q, e=2): 
    n = p * q 
    mp = pow(c, (p + 1) // 4, p) #整除 ⽤// 
    mq = pow(c, (q + 1) // 4, q) 
    yp = gmpy2.invert(p, q) 
    yq = gmpy2.invert(q, p) 
    r = (yp * p * mq + yq * q * mp) % n 
    rr = n - r 
    s = (yp * p * mq - yq * q * mp) % n 
    ss = n - s 
    return (r, rr, s, ss)

c1=62501276588435548378091741866858001847904773180843384150570636252430662080263
c2=72510845991687063707663748783701000040760576923237697638580153046559809128516

p = 275127860351348928173285174381581152299
q = 319576316814478949870590164193048041239
n = p*q
 
temp1 = rabin_decrypt(c1,p,q,2)
temp2 = rabin_decrypt(c2,p,q,2)
for i in temp1:
    print(number.long_to_bytes(i))
for i in temp2:
    print(number.long_to_bytes(i))
#unctf{412a1ed6d21e55191ee5131f266f5178}

共模攻击（Common Modulus Attack)

使用相同的模数n,但是使用了不同的公钥e加密同一明文信息，且公钥中e1,e2应该互质。

方法

结论：当n不变的情况下，知道n,e1,e2,c1,c2 可以在不知道d1,d2情况下，解出m。

证明

由RSA基本原理可知：

由于e1与e2互质，由贝祖等式可知，必有s1,s2满足：

s1,s2皆为整数，但是一正一负，我们可以通过扩展欧几里得算法计算s1,s2

所以：

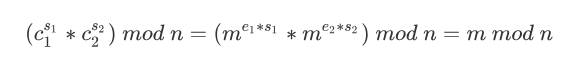
1572264258196

题目积累

very hard RSA(JarvisoJ)

解压下来有三个文件，两个enc文件，和一个加密的python脚本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#veryhrdrsa.py
#!/usr/bin/env/python

import random

N = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929L

def pad_even(x):
	return ('', '0')[len(x)%2] + x
e1 = 17
e2 = 65537
fi = open('flag.txt','rb')
fo1 = open('flag.enc1','wb')
fo2 = open('flag.enc2','wb')

data = fi.read()
fi.close()
while (len(data)<512-11):
	data  =  chr(random.randint(0,255))+data
data_num = int(data.encode('hex'),16)
encrypt1 = pow(data_num,e1,N)
encrypt2 = pow(data_num,e2,N)
fo1.write(pad_even(format(encrypt1,'x')).decode('hex'))
fo2.write(pad_even(format(encrypt2,'x')).decode('hex'))

fo1.close()
fo2.close()

通过算法很容易知道是共模攻击，所以我们不需要的得到密钥d就可以进行解密：

这里出现了一个问题，就是使用gmpy无法进行解密，可能是我脚本写的有问题，目前没有找到解决方案。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import gmpy2
from Crypto.Util import number

N = 0x00b0bee5e3e9e5a7e8d00b493355c618fc8c7d7d03b82e409951c182f398dee3104580e7ba70d383ae5311475656e8a964d380cb157f48c951adfa65db0b122ca40e42fa709189b719a4f0d746e2f6069baf11cebd650f14b93c977352fd13b1eea6d6e1da775502abff89d3a8b3615fd0db49b88a976bc20568489284e181f6f11e270891c8ef80017bad238e363039a458470f1749101bc29949d3a4f4038d463938851579c7525a69984f15b5667f34209b70eb261136947fa123e549dfff00601883afd936fe411e006e4e93d1a00b0fea541bbfc8c5186cb6220503a94b2413110d640c77ea54ba3220fc8f4cc6ce77151e29b3e06578c478bd1bebe04589ef9a197f6f806db8b3ecd826cad24f5324ccdec6e8fead2c2150068602c8dcdc59402ccac9424b790048ccdd9327068095efa010b7f196c74ba8c37b128f9e1411751633f78b7b9e56f71f77a1b4daad3fc54b5e7ef935d9a72fb176759765522b4bbc02e314d5c06b64d5054b7b096c601236e6ccf45b5e611c805d335dbab0c35d226cc208d8ce4736ba39a0354426fae006c7fe52d5267dcfb9c3884f51fddfdf4a9794bcfe0e1557113749e6c8ef421dba263aff68739ce00ed80fd0022ef92d3488f76deb62bdef7bea6026f22a1d25aa2a92d124414a8021fe0c174b9803e6bb5fad75e186a946a17280770f1243f4387446ccceb2222a965cc30b3929

with open('flag.enc1', 'rb') as f:
    c1 = number.bytes_to_long(f.read()) 
with open('flag.enc2', 'rb') as f:
    c2 = number.bytes_to_long(f.read())
e1 = 17
e2 = 65537
print(c1)
_, s1, s2 = gmpy2.gcdext(e1, e2)
if(s1 < 0):
    s1 = -s1
    c1 = gmpy2.invert(c1,N)
if(s2 < 0):
    s2 = -s2
    c2 = gmpy2.invert(c2,N)
res = (pow(c1, s1, N) * pow(c2,s2,N)) % N
print(number.long_to_bytes(res))
#PCTF{M4st3r_oF_Number_Th3ory}

rsappend(jarvisoJ)

解压下来有两个文件，一个python脚本程序，一个可读文本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
flag = open("flag", "r").read().strip()
assert len(flag) == 32

import primefac
import random
from os import urandom
def genprime(l):
    l/=8
    big=1
    while(l):
        big=big<<8
        l-=1
    big-=1
    small=(big+1)>>4
    temp=random.randint(small,big)
    return primefac.nextprime(temp)
def str2num(s):
    return int(s.encode('hex'), 16)
def padding(s):
    return s+urandom(abs(256-len(s)))



def rsappend(m):
    p = genprime(2048)
    q = genprime(2048)
    n = p * q
    result=[str(n)+"\n"]
    pm=padding(flag)
    for i in range(32):  #这里是关键
        e=genprime(32)
        c=pow(str2num(pm),e,n)
        result.append(str(e)+"###"+str(c)+"\n")
    return "".join(result)
open("result","w").write(rsappend(flag))

直接看看关键位置，发现使用不同的e对密文进行了32次加密，但是模数n是相同的，所以这里是共模攻击

第一行数是模数n值，之后每个对应一个密文，只需要两个就可以直接解密

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#coding=utf-8
#owner:IFpop
#time:2019/10/28

import gmpy2
from Crypto.Util import number
N = 130129008900473203968454456805638875182255844172836031362469765750555629223299054613072677100571707156698316733582683118539756860001556017029333867329591302318262912728008327902112481960175532302595162289611406978353816368008691640641366763939266242207191229240305820321249712345088877729541037319788659353057396178127928848886417880913823432701577855911982710310391664759040416918636673098245499680559140960154217578440590540485803953844560093151975252604098243460784073934982164384904788470380402066708313893480356219937915540825156266934523595689350157227336528136089157698775968997579723271988825396396444999743016035145444220925369592263295741687879468786947998534483539986779457827253891091252408156073413533385415338751818544323853074296042153599429749378847870780593975579477549218822682233583377677693108437331184962345568217859524495625257015837972947971787321584159575618388588687948368216479955807108888453821700067186732627409832722329355336479016104249514839541606562090752437124270651936485389358065775555250883907067083447197860848471728871909151915883316674512739238840179296263390441457949281128267215916340163366686542160467601357340644950755337706786366316621293666173843528346692669268972961669116101104865152273

c1 = 95302089605615051645253770338205531172677353498946580682786822045513597212422921981567826452072575982096979591435896082106066368909398510427324124083956090397824543655853708684901332136907086372208856759943292176759073194584568350898675282883285945088425893961769183074018286761903249180704401358403273776903672507958464947244563165564687651203497198317095965140433811056890812018746508121991041040929574993486548175817290824525606551459788553765629416110310419007396912225733599205599864440826319234419035248234403040065378375700430311931418759746223148198205862641252459687694589780856855757703678024583642215076094232444641853081607984934672271461513190437757388818064739151861157236855430066735235471068167602037785718403200529481153399754491247323829122718485697100562237822159608309949585990842201041193231738706398444530233533281604482892716292766323711237917277799500317596333142843576977429802405873159965636003943698854699972663575602383960580472190300576561953143218321528070200681456278974433060654128626428761278953024384187213765974659768657721533448706022075747036347982370028705538843276631102928500802573434484354218539824751579164697748967608238067706842975984077663380114254296902060435479795741671231918448537178

c2 = 105918022590727868761989308441554006325741233318901416621101439141134508212362387984949614887131575960019253866892976283979646611794365370050551871112439674346802340152058463892106629344277362169322187627579360245792142005899616101515519718660483000821415412306495286717542069436530262341500852884860324349096274655178057271529986597578695272732947460673640986877589225588415523871081101162696385279491410034057376225511693022693861779342120101749193614060384925056132593068290214170342896671210026723193650534803792328917982049779674425511275821311773130342656939142955431868128759911406827872932920704284125816103225607727270365652734742083302757644298457617564597237089509337896240249999242834787525341715546373108420197569425092674224333823552432226153066667988737348643469923827028254712179077001007265954488404167147591307425224250970874724864947175449960116685682348915647317191880538777148647712260093008241728509225817352093441924045801257015598517963598799676359095235231066752986688784477694024390356904157694178691411759003004184256950519184836209393583431328640341243629167223114681734264945594931213193459079614652400888215324779908031661350565230685273639666615465296133672907093946148188967451042301308884510424218096

e1 = 3493354673
e2 = 340864687

_, s1, s2 = gmpy2.gcdext(e1, e2)
if(s1 < 0):
    s1 = -s1
    c1 = gmpy2.invert(c1,N)
if(s2 < 0):
    s2 = -s2
    c2 = gmpy2.invert(c2,N)
res = (pow(c1, s1, N) * pow(c2,s2,N)) % N
print(number.long_to_bytes(res))
#flag{we_do_ctf_together_for_fun}

xgm(Jarvisoj)

下载下来有一个txt文件

1
2
3
4
5
6
7
n1=21660190931013270559487983141966347279666044468572000325628282578595119101840917794617733535995976710097702806131277006786522442555607842485975616689297559583352413160087163656851019769465637856967511819803473940154712516380580146620018921406354668604523723340895843009899397618067679200188650754096242296166060735958270930743173912010852467114047301529983496669250671342730804149428700280401481421735184899965468191802844285699985370238528163505674350380528600143880619512293622576854525700785474101747293316814980311297382429844950643977825771268757304088259531258222093667847468898823367251824316888563269155865061
e1=65537
c1=11623242520063564721509699039034210329314238234068836130756457335142671659158578379060500554276831657322012285562047706736377103534543565179660863796496071187533860896148153856845638989384429658963134915230898572173720454271369543435708994457280819363318783413033774014447450648051500214508699056865320506104733203716242071136228269326451412159760818676814129428252523248822316633339393821052614033884661649376604245744651142959498917235138077366818109892738298251161767344501687113868331134288984466294415889635863660753717476594011236542159800099371872396181448655448842148998667568104710807411358117939831241620315

n2=21660190931013270559487983141966347279666044468572000325628282578595119101840917794617733535995976710097702806131277006786522442555607842485975616689297559583352413160087163656851019769465637856967511819803473940154712516380580146620018921406354668604523723340895843009899397618067679200188650754096242296166060735958270930743173912010852467114047301529983496669250671342730804149428700280401481421735184899965468191802844285699985370238528163505674350380528600143880619512293622576854525700785474101747293316814980311297382429844950643977825771268757304088259531258222093667847468898823367251824316888563269155865061
e2=70001
c2=8180690717251057689732022736872836938270075717486355807317876695012318283159440935866297644561407238807004565510263413544530421072353735781284166685919420305808123063907272925594909852212249704923889776430284878600408776341129645414000647100303326242514023325498519509077311907161849407990649396330146146728447312754091670139159346316264091798623764434932753276554781692238428057951593104821823029665203821775755835076337570281155689527215367647821372680421305939449511621244288104229290161484649056505784641486376741409443450331991557221540050574024894427139331416236263783977068315294198184169154352536388685040531

一个简单的共模攻击

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#coding=utf-8
#owner:IFpop
#time:2019/10/28


import gmpy2
from Crypto.Util import number

N = 21660190931013270559487983141966347279666044468572000325628282578595119101840917794617733535995976710097702806131277006786522442555607842485975616689297559583352413160087163656851019769465637856967511819803473940154712516380580146620018921406354668604523723340895843009899397618067679200188650754096242296166060735958270930743173912010852467114047301529983496669250671342730804149428700280401481421735184899965468191802844285699985370238528163505674350380528600143880619512293622576854525700785474101747293316814980311297382429844950643977825771268757304088259531258222093667847468898823367251824316888563269155865061

c1=11623242520063564721509699039034210329314238234068836130756457335142671659158578379060500554276831657322012285562047706736377103534543565179660863796496071187533860896148153856845638989384429658963134915230898572173720454271369543435708994457280819363318783413033774014447450648051500214508699056865320506104733203716242071136228269326451412159760818676814129428252523248822316633339393821052614033884661649376604245744651142959498917235138077366818109892738298251161767344501687113868331134288984466294415889635863660753717476594011236542159800099371872396181448655448842148998667568104710807411358117939831241620315
c2=8180690717251057689732022736872836938270075717486355807317876695012318283159440935866297644561407238807004565510263413544530421072353735781284166685919420305808123063907272925594909852212249704923889776430284878600408776341129645414000647100303326242514023325498519509077311907161849407990649396330146146728447312754091670139159346316264091798623764434932753276554781692238428057951593104821823029665203821775755835076337570281155689527215367647821372680421305939449511621244288104229290161484649056505784641486376741409443450331991557221540050574024894427139331416236263783977068315294198184169154352536388685040531

e1=65537
e2=70001

_, s1, s2 = gmpy2.gcdext(e1, e2)
if(s1 < 0):
    s1 = -s1
    c1 = gmpy2.invert(c1,N)
if(s2 < 0):
    s2 = -s2
    c2 = gmpy2.invert(c2,N)
res = (pow(c1, s1, N) * pow(c2,s2,N)) % N
print(number.long_to_bytes(res))
#flag{gongmogongji}

低加密指数攻击

基本理论

选择小的e可以缩短加密时间，但是选择的e不当，可能会造成严重的安全问题。在CTF题型中，这种攻击一般适用于e=3,

  1. 明文过小，导致明文的三次方还是小于n 

    1
    2
    3
    #此时只需要对密文开三次方即可
    import gmpy2
    gmpy2.iroot(c,e)

  2. 如果m稍微大一点，那么

我们可以对k进行枚举

1
2
3
4
5
6
7
import gmpy2
k = 0
while 1:
    if(gmpy2.iroot(c+k*n,3)[1] == 1):
        print(gmpy2.iroot(c+k*n,3))
        break
     i = i+1

题目积累

Extremely hard RSA(jarvisoj)

解压后发现两个文件，一个密文文件，一个公钥文件，同样使用openssl命令查看公钥信息

1
2
3
4
5
6
7
8
root@DESKTOP-OORTB87:/mnt/c/Users/X1TABLET/Desktop/RSA/extremelyhardRSA# openssl rsa -in pubkey.pem -pubin -text -modulus                   
RSA Public-Key: (4096 bit)             
Modulus:                                           00:b0:be:e5:e3:e9:e5:a7:e8:d0:0b:49:33:55:c6:                         18:fc:8c:7d:7d:03:b8:2e:40:99:51:c1:82:f3:98:                         de:e3:10:45:80:e7:ba:70:d3:83:ae:53:11:47:56:                         56:e8:a9:64:d3:80:cb:15:7f:48:c9:51:ad:fa:65:                         db:0b:12:2c:a4:0e:42:fa:70:91:89:b7:19:a4:f0:                         d7:46:e2:f6:06:9b:af:11:ce:bd:65:0f:14:b9:3c:                         97:73:52:fd:13:b1:ee:a6:d6:e1:da:77:55:02:ab:                         ff:89:d3:a8:b3:61:5f:d0:db:49:b8:8a:97:6b:c2:                         05:68:48:92:84:e1:81:f6:f1:1e:27:08:91:c8:ef:                         80:01:7b:ad:23:8e:36:30:39:a4:58:47:0f:17:49:                         10:1b:c2:99:49:d3:a4:f4:03:8d:46:39:38:85:15:                         79:c7:52:5a:69:98:4f:15:b5:66:7f:34:20:9b:70:                         eb:26:11:36:94:7f:a1:23:e5:49:df:ff:00:60:18:                         83:af:d9:36:fe:41:1e:00:6e:4e:93:d1:a0:0b:0f:                         ea:54:1b:bf:c8:c5:18:6c:b6:22:05:03:a9:4b:24:                         13:11:0d:64:0c:77:ea:54:ba:32:20:fc:8f:4c:c6:                         ce:77:15:1e:29:b3:e0:65:78:c4:78:bd:1b:eb:e0:                         45:89:ef:9a:19:7f:6f:80:6d:b8:b3:ec:d8:26:ca:                         d2:4f:53:24:cc:de:c6:e8:fe:ad:2c:21:50:06:86:                         02:c8:dc:dc:59:40:2c:ca:c9:42:4b:79:00:48:cc:                         dd:93:27:06:80:95:ef:a0:10:b7:f1:96:c7:4b:a8:                         c3:7b:12:8f:9e:14:11:75:16:33:f7:8b:7b:9e:56:                         f7:1f:77:a1:b4:da:ad:3f:c5:4b:5e:7e:f9:35:d9:                         a7:2f:b1:76:75:97:65:52:2b:4b:bc:02:e3:14:d5:                         c0:6b:64:d5:05:4b:7b:09:6c:60:12:36:e6:cc:f4:                         5b:5e:61:1c:80:5d:33:5d:ba:b0:c3:5d:22:6c:c2:                         08:d8:ce:47:36:ba:39:a0:35:44:26:fa:e0:06:c7:                         fe:52:d5:26:7d:cf:b9:c3:88:4f:51:fd:df:df:4a:                         97:94:bc:fe:0e:15:57:11:37:49:e6:c8:ef:42:1d:                         ba:26:3a:ff:68:73:9c:e0:0e:d8:0f:d0:02:2e:f9:                         2d:34:88:f7:6d:eb:62:bd:ef:7b:ea:60:26:f2:2a:                         1d:25:aa:2a:92:d1:24:41:4a:80:21:fe:0c:17:4b:                         98:03:e6:bb:5f:ad:75:e1:86:a9:46:a1:72:80:77:                         0f:12:43:f4:38:74:46:cc:ce:b2:22:2a:96:5c:c3:                         
0b:39:29           
Exponent: 3 (0x3)                                                     Modulus=B0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929                 
writing RSA key                                                       
-----BEGIN PUBLIC KEY-----                                            MIICIDANBgkqhkiG9w0BAQEFAAOCAg0AMIICCAKCAgEAsL7l4+nlp+jQC0kzVcYY      /Ix9fQO4LkCZUcGC85je4xBFgOe6cNODrlMRR1ZW6Klk04DLFX9IyVGt+mXbCxIs      pA5C+nCRibcZpPDXRuL2BpuvEc69ZQ8UuTyXc1L9E7Huptbh2ndVAqv/idOos2Ff      0NtJuIqXa8IFaEiShOGB9vEeJwiRyO+AAXutI442MDmkWEcPF0kQG8KZSdOk9AON      Rjk4hRV5x1JaaZhPFbVmfzQgm3DrJhE2lH+hI+VJ3/8AYBiDr9k2/kEeAG5Ok9Gg      Cw/qVBu/yMUYbLYiBQOpSyQTEQ1kDHfqVLoyIPyPTMbOdxUeKbPgZXjEeL0b6+BF      ie+aGX9vgG24s+zYJsrST1MkzN7G6P6tLCFQBoYCyNzcWUAsyslCS3kASMzdkycG      gJXvoBC38ZbHS6jDexKPnhQRdRYz94t7nlb3H3ehtNqtP8VLXn75NdmnL7F2dZdl      UitLvALjFNXAa2TVBUt7CWxgEjbmzPRbXmEcgF0zXbqww10ibMII2M5HNro5oDVE      JvrgBsf+UtUmfc+5w4hPUf3f30qXlLz+DhVXETdJ5sjvQh26Jjr/aHOc4A7YD9AC      LvktNIj3betive976mAm8iodJaoqktEkQUqAIf4MF0uYA+a7X6114YapRqFygHcP EkP0OHRGzM6yIiqWXMMLOSkCAQM=                                          
-----END PUBLIC KEY-----

下面直接写脚本解密:

ps:gmpy中求根号是gmpy.root gmpy2中求根号是gmpy2.iroot

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#coding=utf-8
import gmpy2
from Crypto.Util import number

with open('flag.enc','rb') as f:
    c = number.bytes_to_long(f.read()) 
print(c)
n = int('0xB0BEE5E3E9E5A7E8D00B493355C618FC8C7D7D03B82E409951C182F398DEE3104580E7BA70D383AE5311475656E8A964D380CB157F48C951ADFA65DB0B122CA40E42FA709189B719A4F0D746E2F6069BAF11CEBD650F14B93C977352FD13B1EEA6D6E1DA775502ABFF89D3A8B3615FD0DB49B88A976BC20568489284E181F6F11E270891C8EF80017BAD238E363039A458470F1749101BC29949D3A4F4038D463938851579C7525A69984F15B5667F34209B70EB261136947FA123E549DFFF00601883AFD936FE411E006E4E93D1A00B0FEA541BBFC8C5186CB6220503A94B2413110D640C77EA54BA3220FC8F4CC6CE77151E29B3E06578C478BD1BEBE04589EF9A197F6F806DB8B3ECD826CAD24F5324CCDEC6E8FEAD2C2150068602C8DCDC59402CCAC9424B790048CCDD9327068095EFA010B7F196C74BA8C37B128F9E1411751633F78B7B9E56F71F77A1B4DAAD3FC54B5E7EF935D9A72FB176759765522B4BBC02E314D5C06B64D5054B7B096C601236E6CCF45B5E611C805D335DBAB0C35D226CC208D8CE4736BA39A0354426FAE006C7FE52D5267DCFB9C3884F51FDDFDF4A9794BCFE0E1557113749E6C8EF421DBA263AFF68739CE00ED80FD0022EF92D3488F76DEB62BDEF7BEA6026F22A1D25AA2A92D124414A8021FE0C174B9803E6BB5FAD75E186A946A17280770F1243F4387446CCCEB2222A965CC30B3929',16)
print(n)
k = 0
while 1:
    if(gmpy2.iroot(c+k*n,3)[1] == 1):
        m = gmpy2.iroot(c+k*n,3)
        print(m[0])
        print(number.long_to_bytes(m[0]))
        break
    k = k + 1
#PCTF{Sm4ll_3xpon3nt_i5_W3ak}
#可能需要的时间有点长
#看网上的wp，发现k>118000000
#可将k = 118000000加快速度

xbk(Jarvisoj)

1
2
3
n=47966708183289639962501363163761864399454241691014467172805658518368423135168025285144721028476297179341434450931955275325060173656301959484440112740411109153032840150659
e=3
c=10968126341413081941567552025256642365567988931403833266852196599058668508079150528128483441934584299102782386592369069626088211004467782012298322278772376088171342152839

解密脚本:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#coding=utf-8
#owner:IFpop
#time:2019/10/28

import gmpy2
from Crypto.Util import number

c = 10968126341413081941567552025256642365567988931403833266852196599058668508079150528128483441934584299102782386592369069626088211004467782012298322278772376088171342152839
n = 47966708183289639962501363163761864399454241691014467172805658518368423135168025285144721028476297179341434450931955275325060173656301959484440112740411109153032840150659
k = 0
while 1:
    if(gmpy2.iroot(c+k*n,3)[1] == 1):
        m = gmpy2.iroot(c+k*n,3)
        print(m[0])
        print(number.long_to_bytes(m[0]))
        break
    k = k + 1
#flag{let_me_do_sth_good}

选择密文攻击

题目记录

打开链接看到三个选项，很明显可以使用选择密文攻击

  1. 首先要让其r < n，r = 2，加密值如下,记为x, :

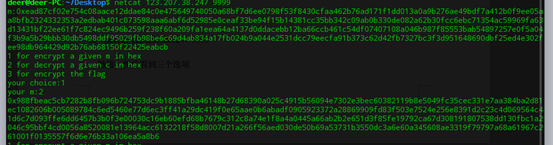
1572939810162

  1. 然后读出flag的密文值,记为c, ：

    1572939865771

  2. 将flag的密文与m的密文相乘，然后模n,得到­y, ,又因为chice2是有解密的，所以将y解密得到下面一行,记为u,

    1572939891298

    由RSA原理可知

    m = u//r#这里的//代表整除

    大致脚本如下

    1
    2
    3
    4
    5
    #coding:utf-8
    from Crypto.Util import number
    data = 0xd2e6d8c2c4f6a4a682bed26abeec6ae4f2becac2f4f4f4f4f2fa//2  #整除
    m = number.long_to_bytes(data)
    print(m)

    得到flag: islab{RSA_i5_v5ry_eazzzzy}

私钥恢复和最优非对称加密填充

基本理论

私钥重构

题目积累

GOD LIKE RSA(jarvisoj)

解压之后，有三个文件，一个公钥文件，一个密文文件，一个损坏的私钥文件

查看公钥信息：

1
RSA Public-Key: (4096 bit)                                                              Modulus:                                                                               00:c0:97:78:53:45:64:84:7d:8c:c4:b4:20:e9:33:                                           58:67:ec:78:3e:6c:f5:f0:5c:a0:3e:ee:dc:25:63:                                           d0:eb:2a:9e:ba:8f:19:52:a2:67:0b:e7:6e:b2:34:                                           b8:6d:50:76:e0:6a:d1:03:cf:77:33:d8:b1:e9:d7:                                           3b:e5:eb:1c:65:0c:25:96:fd:96:20:b9:7a:de:1d:                                           bf:fd:f2:b6:bf:81:3e:3e:47:44:43:98:bf:65:2f:                                           67:7e:27:75:f9:56:47:ba:c4:f0:4e:67:2b:da:e0:                                           1a:77:14:40:29:c1:a8:67:5a:8f:f5:2e:be:8e:82:                                           31:3d:43:26:d4:97:86:29:15:14:a9:69:36:2c:76:                                           ed:b5:90:eb:ec:6f:ce:d5:ca:24:1c:aa:f6:63:f8:                                           06:a2:62:cb:26:74:d3:5b:82:4b:b6:d5:e0:49:32:                                           7b:62:f8:05:c4:f7:0e:86:59:9b:f3:17:25:02:aa:                                           3c:97:78:84:7b:16:fd:1a:f5:67:cf:03:17:97:d0:                                           c6:69:85:f0:8d:fa:ce:ee:68:24:63:06:24:e1:e4:                                           4c:f8:e9:ad:25:c7:e0:c0:15:bb:b4:67:48:90:03:                                           9b:20:7f:0c:17:eb:9d:13:44:ab:ab:08:a5:c3:dc:                                           c1:98:88:c5:ce:4f:5a:87:9b:0b:bf:bd:d7:0e:a9:                                           09:59:81:fa:88:4f:59:60:6b:84:84:ad:d9:c7:25:                                           8c:e8:c0:e8:f7:26:9e:37:95:7c:e1:48:29:0f:51:                                           e7:bd:98:2f:f6:cc:80:e7:f0:32:0b:89:51:92:4e:                                           c2:6d:50:53:2b:3b:77:72:d1:bd:1a:1f:92:d7:12:                                           79:61:61:c5:a4:7e:b3:85:eb:f0:7c:6d:46:03:c5:                                           e6:d5:81:2c:ba:7e:ea:8d:51:7d:63:55:34:2a:b6:                                           d4:dc:31:5a:f1:99:e3:dc:8c:83:0b:a2:2a:d5:3c:                                           41:48:41:54:1a:a9:e8:b6:70:bf:d3:fe:ed:19:17:                                           14:94:13:b3:17:e3:8b:8e:6f:53:ed:e2:44:e8:4a:                                           32:d6:5c:0d:a8:80:f5:fc:02:e9:46:55:d5:a4:d3:                                           e7:c6:30:77:f9:73:e9:44:52:d8:13:9d:5d:bf:9e:                                           fa:3a:b5:96:79:82:5b:cd:19:5c:06:a9:00:96:fd:                                           4c:a4:73:88:1a:ec:3c:11:de:b9:3d:e0:50:00:1e:                                           ac:21:97:a1:96:7d:6b:15:f9:6c:c9:34:7f:70:d7:                                           9d:2d:d1:48:4a:81:71:f8:12:dd:32:ba:64:31:60:                                           08:26:4b:09:22:03:83:90:17:7f:f3:a7:72:57:bf:                                           89:6d:e4:d7:40:24:8b:7b:bd:df:33:c0:ff:30:2e:                                           e8:6c:1d                                                                               Exponent: 65537 (0x10001)                                                                                               Modulus=C09778534564847D8CC4B420E9335867EC783E6CF5F05CA03EEEDC2563D0EB2A9EBA8F1952A2670BE76EB234B86D5076E06AD103CF7733D8B1E9D73BE5EB1C650C2596FD9620B97ADE1DBFFDF2B6BF813E3E47444398BF652F677E2775F95647BAC4F04E672BDAE01A77144029C1A8675A8FF52EBE8E82313D4326D49786291514A969362C76EDB590EBEC6FCED5CA241CAAF663F806A262CB2674D35B824BB6D5E049327B62F805C4F70E86599BF3172502AA3C9778847B16FD1AF567CF031797D0C66985F08DFACEEE6824630624E1E44CF8E9AD25C7E0C015BBB4674890039B207F0C17EB9D1344ABAB08A5C3DCC19888C5CE4F5A879B0BBFBDD70EA9095981FA884F59606B8484ADD9C7258CE8C0E8F7269E37957CE148290F51E7BD982FF6CC80E7F0320B8951924EC26D50532B3B7772D1BD1A1F92D712796161C5A47EB385EBF07C6D4603C5E6D5812CBA7EEA8D517D6355342AB6D4DC315AF199E3DC8C830BA22AD53C414841541AA9E8B670BFD3FEED1917149413B317E38B8E6F53EDE244E84A32D65C0DA880F5FC02E94655D5A4D3E7C63077F973E94452D8139D5DBF9EFA3AB59679825BCD195C06A90096FD4CA473881AEC3C11DEB93DE050001EAC2197A1967D6B15F96CC9347F70D79D2DD1484A8171F812DD32BA64316008264B0922038390177FF3A77257BF896DE4D740248B7BBDDF33C0FF302EE86C1D             writing RSA key                                                                         -----BEGIN PUBLIC KEY-----                                                                                            MIICIjANBgkqhkiG9w0BAQEFAAOCAg8AMIICCgKCAgEAwJd4U0VkhH2MxLQg6TNY                                                        Z+x4Pmz18FygPu7cJWPQ6yqeuo8ZUqJnC+dusjS4bVB24GrRA893M9ix6dc75esc                                                        ZQwllv2WILl63h2//fK2v4E+PkdEQ5i/ZS9nfid1+VZHusTwTmcr2uAadxRAKcGo                                                        Z1qP9S6+joIxPUMm1JeGKRUUqWk2LHbttZDr7G/O1cokHKr2Y/gGomLLJnTTW4JL                                                        ttXgSTJ7YvgFxPcOhlmb8xclAqo8l3iEexb9GvVnzwMXl9DGaYXwjfrO7mgkYwYk                                                        4eRM+OmtJcfgwBW7tGdIkAObIH8MF+udE0Srqwilw9zBmIjFzk9ah5sLv73XDqkJ                                                        WYH6iE9ZYGuEhK3ZxyWM6MDo9yaeN5V84UgpD1HnvZgv9syA5/AyC4lRkk7CbVBT                                                        Kzt3ctG9Gh+S1xJ5YWHFpH6zhevwfG1GA8Xm1YEsun7qjVF9Y1U0KrbU3DFa8Znj                                                        3IyDC6Iq1TxBSEFUGqnotnC/0/7tGRcUlBOzF+OLjm9T7eJE6Eoy1lwNqID1/ALp                                                        RlXVpNPnxjB3+XPpRFLYE51dv576OrWWeYJbzRlcBqkAlv1MpHOIGuw8Ed65PeBQ                                                        AB6sIZehln1rFflsyTR/cNedLdFISoFx+BLdMrpkMWAIJksJIgODkBd/86dyV7+J                       beTXQCSLe73fM8D/MC7obB0CAwEAAQ==                                                       -----END PUBLIC KEY-----

模数n有4096bit，分解不太现实，所以目前还是使用损坏的私钥文件，修复脚本(具体也能在基本理论的链接中找到)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
#!/usr/bin/python3

import re
from itertools import product
from Crypto.Util.number import GCD, inverse


def solve_linear(a, b, mod):
    if a & 1 == 0 or b & 1 == 0:
        return None
    return (b * inverse(a, mod)) & (mod - 1)  # 计算b*a^(-1)%mod


def to_n(s):
    s = re.sub(r"[^0-9a-f]", "", s)
    return int(s, 16)


def msk(s):
    cleaned = "".join(map(lambda x: x[-2:], s.split(":")))   #去掉冒号和多余字符和空格
    return msk_ranges(cleaned), msk_mask(cleaned), msk_val(cleaned)


def msk_ranges(s):      #    求每一个半字节的取值范围
    return [range(16) if c == " " else [int(c, 16)] for c in s]    


def msk_mask(s):
    return int("".join("0" if c == " " else "f" for c in s), 16)


def msk_val(s):
    return int("".join("0" if c == " " else c for c in s), 16)


N = to_n("""\
00:c0:97:78:53:45:64:84:7d:8c:c4:b4:20:e9:33:
58:67:ec:78:3e:6c:f5:f0:5c:a0:3e:ee:dc:25:63:
d0:eb:2a:9e:ba:8f:19:52:a2:67:0b:e7:6e:b2:34:
b8:6d:50:76:e0:6a:d1:03:cf:77:33:d8:b1:e9:d7:
3b:e5:eb:1c:65:0c:25:96:fd:96:20:b9:7a:de:1d:
bf:fd:f2:b6:bf:81:3e:3e:47:44:43:98:bf:65:2f:
67:7e:27:75:f9:56:47:ba:c4:f0:4e:67:2b:da:e0:
1a:77:14:40:29:c1:a8:67:5a:8f:f5:2e:be:8e:82:
31:3d:43:26:d4:97:86:29:15:14:a9:69:36:2c:76:
ed:b5:90:eb:ec:6f:ce:d5:ca:24:1c:aa:f6:63:f8:
06:a2:62:cb:26:74:d3:5b:82:4b:b6:d5:e0:49:32:
7b:62:f8:05:c4:f7:0e:86:59:9b:f3:17:25:02:aa:
3c:97:78:84:7b:16:fd:1a:f5:67:cf:03:17:97:d0:
c6:69:85:f0:8d:fa:ce:ee:68:24:63:06:24:e1:e4:
4c:f8:e9:ad:25:c7:e0:c0:15:bb:b4:67:48:90:03:
9b:20:7f:0c:17:eb:9d:13:44:ab:ab:08:a5:c3:dc:
c1:98:88:c5:ce:4f:5a:87:9b:0b:bf:bd:d7:0e:a9:
09:59:81:fa:88:4f:59:60:6b:84:84:ad:d9:c7:25:
8c:e8:c0:e8:f7:26:9e:37:95:7c:e1:48:29:0f:51:
e7:bd:98:2f:f6:cc:80:e7:f0:32:0b:89:51:92:4e:
c2:6d:50:53:2b:3b:77:72:d1:bd:1a:1f:92:d7:12:
79:61:61:c5:a4:7e:b3:85:eb:f0:7c:6d:46:03:c5:
e6:d5:81:2c:ba:7e:ea:8d:51:7d:63:55:34:2a:b6:
d4:dc:31:5a:f1:99:e3:dc:8c:83:0b:a2:2a:d5:3c:
41:48:41:54:1a:a9:e8:b6:70:bf:d3:fe:ed:19:17:
14:94:13:b3:17:e3:8b:8e:6f:53:ed:e2:44:e8:4a:
32:d6:5c:0d:a8:80:f5:fc:02:e9:46:55:d5:a4:d3:
e7:c6:30:77:f9:73:e9:44:52:d8:13:9d:5d:bf:9e:
fa:3a:b5:96:79:82:5b:cd:19:5c:06:a9:00:96:fd:
4c:a4:73:88:1a:ec:3c:11:de:b9:3d:e0:50:00:1e:
ac:21:97:a1:96:7d:6b:15:f9:6c:c9:34:7f:70:d7:
9d:2d:d1:48:4a:81:71:f8:12:dd:32:ba:64:31:60:
08:26:4b:09:22:03:83:90:17:7f:f3:a7:72:57:bf:
89:6d:e4:d7:40:24:8b:7b:bd:df:33:c0:ff:30:2e:
e8:6c:1d""")

p_ranges, pmask_msk, pmask_val = msk("""\
 0: e:  :  :  :c :c :  :  :  :b :  :  :  :  :
  :ab: e: 2: 8:c :  :  : 1:6 :6 : 6: f:d9: 0:
8 :5c:7 :06:  :  :  :0 : 3:5 :4b:  :6 :  :  :
2 :  :6 :  :  :  :2 :bc: c:  :85:1 : 1:d : 3:
 1:b4:  : b: 1: 3: d:a :  :  :6e: 0:b :2 :  :
  :b :  :9 :e :  :82:8d:  :  :13:  :  : a: a:
  :  :4 :  :c : f:  :  :7 :e :0a:  :  : b: 5:
  : e:91:3 :  :3c: 9:  : 6:  :  :b5:7d: 1:  :
  :  :  :b :a1:99:6 :4 :3 :c :1a:02:4 :  : 9:
9 :f : d:bd:  :0 :  :  :  :b3:  : 4:  :e9: 9:
  : d:  :  :7 :  :93:  : e:dc:  : 0:  :e7:  :
e :  :2 : b: 2:5 :  :  :  :  : c:5f:  :  :e2:
  :  : 9:  :2a:  : e:  :  :2 :  :9f: 7:3 :  :
b : f:b :  : 8: 7:  :  :f :6 :e :c :  :3 :  :
f7: 5: 8: 5:  :  :  :  :  : 8: e:  :03: c:  :
33:76:e : 1:7 : c:  : 0:  :0b:  : a:  : 2: 9:
  :c8:bf:  :  :06: 7:d5:  :02: c:b :e2: 7:2 :
  :  """)

q_ranges, qmask_msk, qmask_val = msk("""\
 0: f:  :d0: 1:55: 4:31:  : b:c4:8 :  : e: d:
34: 3:f :  :  :  :  : 8:99:1 :  : a:0 :  :4 :
0 :  :f :  :a4:41:2 :  :a :  : 1:  : a: c:  :
  :  : 9:  :  : 2:f4: f:  :  :  :  :1 : 4:9 :
a :  :  :79:0 :  :  :  :  : 2: 8:b :  :4 : 8:
  :9b: 1:  :d :  :f :e4:  :4 :c :e :  :3 :  :
 7:2 :  :d :8 :2 :7 :  :d :67:fc:e : 0:f9: 7:
8 :  :  :  :1 :2f:  :51:  :  :2e:0a: e:3d: 6:
b :  :dd:  : 0:fb:  :f4:  :  :  :b4: 9:c :  :
 a:  :  :  :d :  :  :6b: 2:  :9b: a:60:  :d6:
 0:4f:16:d1:  :  :5 :fc:  :f :  :8 :  :  :  :
 1: 6:e1:9 : e:4 : 6: c: d:d :73: 3:  :  :7 :
  :8 : 9:  :3b:f : 2:  :  :f1: e:  :  :1e:  :
8 :  :  : 6:0 : 4:99:e :  : 5:  :  : 4:  :  :
  : a:81:64:  :7 :f : 9: d:  :9 :  : 7:93:f :
ac:8c:  : 8:  : 0: d: 8:  :7 :  :1d:  :f :  :
1 :a :6 :8 :  :60:  :b3:  :  :  :89:  :  :14:
  :5 """)


_, dmask_msk, dmask_val = msk("""\
  :  :  : f:8 :a5:d : 2: 0:b :7 :  : 1:  : 4:
 1:0d:  :3 :  :6 :  :  : b:  :  :  :e :  :  :
0e: 0:db:  :1a:1c:c0:  : e:  :  :99:bc:8 :a5:
7 :7 :7 : b:  :  : 8: 8:  :7 :55: 2:  :  :f :
b2:  :  :b :f :4 :  : 8:  :b :  :  :  : 0:  :
0 :  :6 :9 :  :  :  : b: 4:  : 0: a: 5:07:b :
 9: c:9a: 9:  : 7:9e:  : b:60:f :  :  :  :0 :
  : 3:0 :  :  :  : 1:b :  :  : b: 6:0 :f :  :
  : 2:18: 6: b:1 :  :  :  :  :d3:f3:  :a :  :
 3:  :  :  :  : 3: d: 1: 2:7 :  : d:  : 2: d:
  :  : d:4 :  :d :  :6d: c:a :b6:  :  :  : 1:
69:  : 7:  :89:  :c :8 :61: d:25: 3:7 :1b: 4:
b :  :8 :55:  :49: 1:2 :3 :  :1 :e9:a8: 3:  :
9 :  : 1:f8:d3:  :e :  :d :  :9 :b6:  :  :71:
1 :  :c1:  : b: 1:  : 6:e :  :64:  :  :1a:c :
  : b:  :bf:c :  : 0:  : 8:a :4 :  :26:a :5 :
6 :  :  :  :eb:  :e5: a:  :3e:f9:10:0 :  :  :
 6:0 :  : 8:  : 1:72: c:0 : f:5 : f:9c: 0: e:
 7:b :  :  :  :  :d9: 4:  : e:c :68:  :  :  :
 c:  :3a:  :  :a0:ea: 3: 4:  :72:a :d : 8:  :
  :0d:5 :0 : a: 7:c :bb: 6: 4:a :ce:d :2 : 1:
  :  :17:6 :  : c: b:  : f:  :3 : 5:6 :3 :0e:
  : 7:c :3e: 2: 9: 7: 6: f: e: f: 9:  :f3: 9:
a :c1:6 :  : 1:9 :  :43:  : f: 5:  :0 :27: 4:
4 :a :  :e9:  : 8: 4:3 :8a: 6:16:d5:c : e: e:
  :d : c:b :a8:  : 7:  : 9:  :7 :7d:  :  :  :
  :  :  :4 :2 :  : 3: 3: 6:  :  :  :7b:0 :  :
 e:  :0 :  :a :  : 5:  :  :  : 5:1 :82:c :0d:
4 :2 :fd:36: 5:50:0 :  :  :d : f: 6:  :  :e :
0 :  :  :ce:  :9e:8 :  :0 :d :07:b3:  :  :  :
0 :e4:  :  :68:b :c :  : c:5 :  :  :3 : 7: 2:
 c:e0:  :5 :  :  :b4:  :ef: 7:  :1 :e : 0:f :
  :6 :  :  :  :e0:c :3 :  :  : 3:  : d:  :  :
 3: 3: c: a:  :b : a:71: 3: 0:a :  :4 :5d:  :
0 :4 """)


_, dpmask_msk, dpmask_val = msk("""\
  : 3:2a:  : d:  :  :  :  :0 :1 : f:  :  : 6:
1 :2 :1b:07: a:e :b :c5:58:7 :  :e8: 7: 1: c:
  : 1:b :a0: 4:0f:5 :67:  :3 :7 :6 :f9:  : c:
  :79: 0:1 :65:  :8 :  :99: d:d :  :2 :9 :0 :
 e:  :0 :  :  :  : d:  :d :7 :6 :a9: a:8b: b:
  :  : 7: a:37:  :  :7 :1 :6 :  :c2: 7:6 :b :
 e:  :  :  :  :  :  :b :3a:5 :  :  :  :  :  :
  :  :  :cd:8 :  : d:  :7 : 3:  : f:e : c:  :
  : a:  :c : f:c : 7:b :5 :  :  :2 :8 :8 :6 :
0a: a:  :  :3 :db:  : 4:00:  : d:  :b : 5:  :
20: 2: 5:  :82:  : 0: 6:  :8a:  :7 :  : 8:  :
 4: 1:  :  :  : 8:46:  :  :  :  :  : 0:f :c8:
2 :  : c:7 :  : 1:  :  :2 : 0: 5:  :  : 1:9b:
 6:9 : 0:74:  :c :  :e :  :  :cb:b :3 :3 :  :
 2:  :  :47:  :2 : 0:5 :  :  : d: 6:83:  :  :
  :c7:  :  :0b:  :  : c:  :3 :8 :  :9 :4 : 7:
5 :c0:fe:  :f9: 1:  :0 : e: 8:02:  : f:  :c :
55:61""")

_, dqmask_msk, dqmask_val = msk("""\
  :0b:7 :4 :0 : 0:6 : 7:7e:  : 5:  : 7:  : a:
a :d : 0: 6: 4:86:  :  :8 :  :  :  :  :e :8f:
 9:  :  :  : 1:  :2 :  : 7: b:1 :5 : f:  :8 :
  :d :21:  :e : d:  :c9:e : b:  :  :1 :  :  :
  :d :a2:b7:  :  :  :f3:  :42:  :e : c:  :f :
  : 0:f :7 : 4: 5:34:  :4 : c:  :  :8 :d : 8:
5 :af: 3:1d: 5:4 :  :2 :  :6 :c : 6:a :1 :5 :
 a:9 :  :d :  :  :0a:a1:  :f :7 :9 :b :  :  :
 f:2 :27: f:  :0 :f6:4d:  :  :  :  :  :5 :  :
 4:08:  : 5:  : 8: 5:  :  :  :18: 4: 8:57: 2:
 f: a:  :  :a8: f: c:f : e: 1:9 :c : 4:9 :  :
  :  :  :  :  : 1:  :2 :  :d1:  : 6:e : d:  :
  : f:04:2 :8d:  : 3:  :  :b : 8:  :d6:  : 2:
  :  :  :6 :  : f:  :  : 0:6 :  :51:  :48:19:
  :  :  :69:4 : c:  :c :  : f:  :f4:d :  : f:
 d:0 :0d:b :3 : 3:2 :  :  :6 : b:5 :2 :  : c:
 1:5a: f:f :  :  :7e:3e:  :d :f :0 : d: c: 6:
 1""")


E = 0x10001

def search(K, Kp, Kq, check_level, break_step):
    max_step = 0
    cands = [0] # 广搜队列
    for step in range(1, break_step + 1):
        # step代表复原倒数第step步
        max_step = max(step, max_step)

        mod = 1 << (4 * step)
        mask = mod - 1

        cands_next = []
        for p, new_digit in product(cands, p_ranges[-step]):
            pval = (new_digit << ((step - 1) * 4)) | p

            # 四个剪枝
            if check_level >= 1:
                qval = solve_linear(pval, N & mask, mod)
                if qval is None or not check_val(qval, mask, qmask_msk, qmask_val):
                    continue

            if check_level >= 2:
                val = solve_linear(E, 1 + K * (N - pval - qval + 1), mod)
                if val is None or not check_val(val, mask, dmask_msk, dmask_val):
                    continue

            if check_level >= 3:
                val = solve_linear(E, 1 + Kp * (pval - 1), mod)
                if val is None or not check_val(val, mask, dpmask_msk, dpmask_val):
                    continue

            if check_level >= 4:
                val = solve_linear(E, 1 + Kq * (qval - 1), mod)
                if val is None or not check_val(val, mask, dqmask_msk, dqmask_val):
                    continue

                if pval * qval == N: #得到答案
                    print("Kq =", Kq)
                    print("pwned")
                    print("p =", pval)
                    print("q =", qval)
                    p = pval
                    q = qval
                    d = inverse(E, (p - 1) * (q - 1))
                    print("d =", d)
                    coef = inverse(p, q)

                    from Crypto.PublicKey import RSA
                    print(RSA.construct((N, E, d, p, q, coef)).exportKey().decode())
                    quit()

            cands_next.append(pval)

        if not cands_next:
            return False
        cands = cands_next
    return True


def check_val(val, mask, mask_msk, mask_val):
    test_mask = mask_msk & mask
    test_val = mask_val & mask
    return val & test_mask == test_val



for K in range(1, E):
    if K % 100 == 0:
        print("checking", K)
    if search(K, 0, 0, check_level=2, break_step=20):
        print("K =", K)
        break

for Kp in range(1, E):
    if Kp % 1000 == 0:
        print("checking", Kp)
    if search(K, Kp, 0, check_level=3, break_step=30):
        print("Kp =", Kp)
        break

for Kq in range(1, E):
    if Kq % 100 == 0:
        print("checking", Kq)
    if search(K, Kp, Kq, check_level=4, break_step=9999):
        print("Kq =", Kq)
        break

然后使用openssl进行解密，此处加密填充方式使用的是OAEP padding方式，所以解密时应该注意：

1
openssl rsautl -decrypt -inkey private.pem -keyform PEM -in flag.enc -oaep

或者写脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# coding=utf-8
from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP
from Crypto.Util import number

with open('pubkey.pem', 'rb') as f:
    key = RSA.importKey(f.read())
    N = key.n
    e = key.e

with open('private.pem', 'rb') as f:
    private = RSA.importKey(f.read())
    oaep = PKCS1_OAEP.new(private)

with open('flag.enc', 'rb') as f:
    print(oaep.decrypt(f.read()).decode())

Openssl使用

openssl命令

  1. 查看公钥pem信息

    1
    openssl rsa -in pubkey.pem -pubin -text -modulus

  2. 利用生成私钥解密

    1
    openssl rsautl -decrypt -inkey pkey -in flag.enc -out out.txt

  3. 生成私钥

    1
    openssl asn1parse -genconf [config file] -out newkey.der

  4. 更多

Medium RSA——Jarvis OJ

方法一

解压后发现了两个文件，一个.pem文件，一个.enc文件

1
2
RSA Public-Key: (256 bit)                                                                  Modulus:                             
00:c2:63:6a:e5:c3:d8:e4:3f:fb:97:ab:09:02:8f:                                            1a:ac:6c:0b:f6:cd:3d:70:eb:ca:28:1b:ff:e9:7f:                                             be:30:dd                                                                                  Exponent: 65537 (0x10001)                                               Modulus=C2636AE5C3D8E43FFB97AB09028F1AAC6C0BF6CD3D70EBCA281BFFE97FBE30DD                 writing RSA key                                                                           -----BEGIN PUBLIC KEY-----                                                                MDwwDQYJKoZIhvcNAQEBBQADKwAwKAIhAMJjauXD2OQ/+5erCQKPGqxsC/bNPXDr         	 yigb/+l/vjDdAgMBAAE=                                                                     -----END PUBLIC KEY-----

使用yafu对模数进行分解得到

1
2
p = 275127860351348928173285174381581152299    
q = 319576316814478949870590164193048041239

解密脚本：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
#coding=utf-8
import rsa
import gmpy

e = 65537
n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
p = 275127860351348928173285174381581152299  
q = 319576316814478949870590164193048041239
fn = (p-1)*(q-1)

d = int(gmpy.invert(e,fn))
privateKey = rsa.PrivateKey(n,e,d,p,q) 
with open("flag.enc","rb") as f:
    print(rsa.decrypt(f.read(),privateKey).decode())
#PCTF{256b_i5_m3dium}

方法二

使用RSAtools或者脚本生成密钥文件，使用openssl解密，

私钥生成脚本:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#coding=utf-8
import math
from Crypto.PublicKey import RSA
import gmpy
#生成一个1024位的私钥
pri = RSA.generate(1024)
pri.e = 65537
pri.n = 87924348264132406875276140514499937145050893665602592992418171647042491658461
pri.p = 275127860351348928173285174381581152299  
pri.q = 319576316814478949870590164193048041239
fn = (pri.p-1)*(pri.q-1)

pri.d = int(gmpy.invert(pri.e,fn))

private = open('private.pem','w')
private.write(pri.exportKey())
private.close()

使用

1
openssl rsautl -decrypt -inkey private.pem -in flag.enc -out out.txt

得到PCTF{256b_i5_m3dium}

-------------本文结束感谢您的阅读-------------
0%