Sudoku

项目链接

数独项目仓库

PSP

PSP是卡耐基梅隆大学（CMU）的专家们针对软件工程师所提出的一套模型：Personal Software Process (PSP， 个人开发流程，或称个体软件过程)。

时间安排表

PSP2.1	Personal Software Process stages	预估耗时(min)	实际耗时(min)
Planning	计划	60	60
·Estimate	·估计这个任务需要多少时间	60*48	60*72
Development	开发	60*2	60*5
· Analysis	· 需求分析 (包括学习新技术)	60*2	60*3
· Design Spec	· 生成设计文档	60	60
· Design Review	· 设计复审	60*2	60
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	60	60*3
· Design	· 具体设计	60*3	60
· Coding	· 具体编码	60*4	60*3
· Code Review	· 代码复审	60*2	60*2
· Test	· 测试（自我测试，修改代码，提交修改）	60*4	60*3
Reporting	报告	60*3	60*1
· Test Repor	· 测试报告	60	30
· Size Measurement	· 计算工作量	60	30
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	60*2	60
	合计	60*77	60*101

需求分析

• 生成终局

  • 在命令行中使用-c参数加数字N(1≤N≤1000000)控制生成数独终局的数量

    sudoku.exe -c N

  • 将生成的数独终局用一个文本文件(假设名字叫sudoku.txt)的形式保存起来，每次生成的txt文件需要覆盖上次生成的txt文件，文件内的格式如下，数与数之间由空格分开，终局与终局之间空一行，行末无空格

  • 程序在处理命令行参数时，不仅能处理格式正确的参数，还能处理各种异常的情况，如：

    sudoku.exe -c abc

  • 在生成数独矩阵时，左上角的第一个数为：(学号后两位相加)%9+1。

• 求解数独

  • 在命令行中使用-s参数加文件名的形式求解数独，并将结果输出至文件，如：

    sudoku.exe -s absolute_path_of_puzzlefile

    程序将从路径中读取数独题目，并将数独题目的一个可行解输出至sudoku.exe同目录的sudoku.txt，要求与生成终局相同。

  • 数独题目格式：其中0代表空格，题目与题目之间空一行，行末无空格，最后一个数独题目后无空行。

  • 数独题目个数N(1≤N≤1000000)，保证文件中的数独格式正确。

• 其他要求

  • 需要对代码进行一定的注释。
  • 要求程序在60s内给出结果。

解题思路

生成终局

方法

根据题述要求，先确定如何生成终局。通过网上查资料，得到如下方法：

• 回溯法

  从数独的左上角(0,0)处开始，生成随机数，然后依次从左往右、从上往下，在某一步生成1-9的数字均不能满足数独要求的时候需要退回到上一个状态重新生成其他可能的解，如此直至最终拼成完整的数独地图。

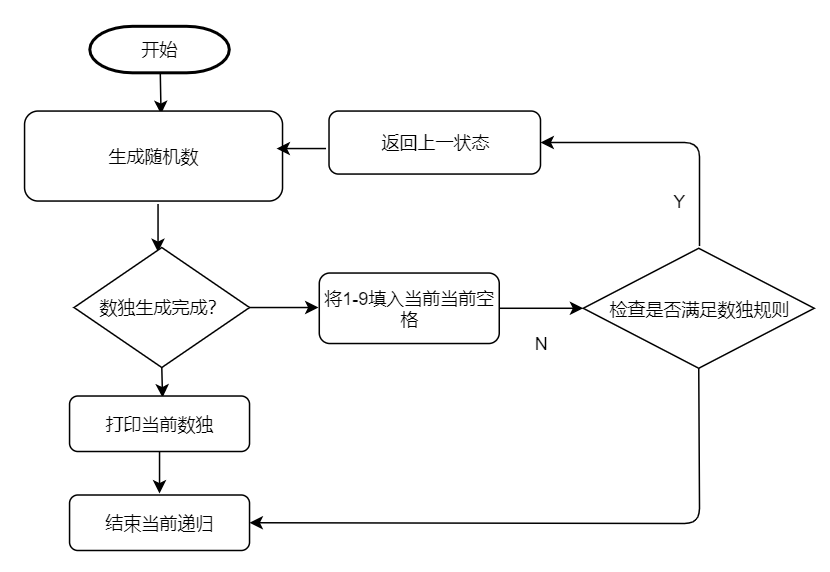
• 以宫为单位的矩阵置换法

  • 第一步：先在第五宫填完一个满足数独要求的9个数字

  

  • 第二步：将第五宫内容通过行变换放置到左边和右边的两个九宫格

  

  • 第三步：将第五宫的九宫格内容通过列变换放置上边和下边的两个九宫格

  

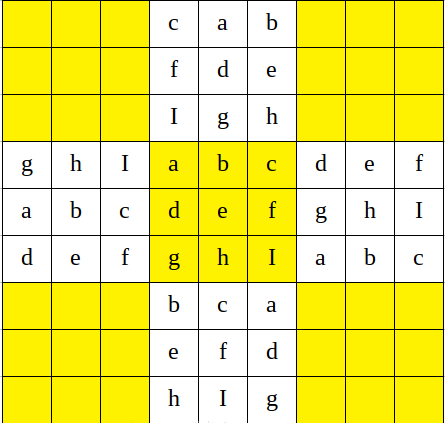
  • 第四步：将第4宫的九宫格内容通过列变换放置到上边和下边的两个九宫格，将第6宫的九宫格内容也通过列变换放置到上边和下边的两个九宫格。

  

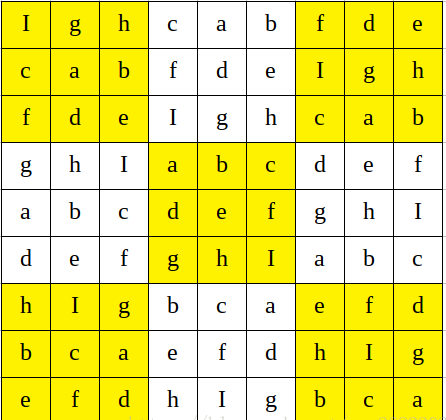
• 模板数字替换法

  事先准备好一个符合要求的数独终局模板，模板中的元素为字母a~i，然后随机生成一串包含1-9的数字序列，将字母一一对应，替换为数字，获得数独终局。

• 数列法

  生成一个数列，然后将此数列分别向右移动0、3、6、1、4、7、2、5、8位得到终局第一到第九行。可以将第1~3行对应的移动位数改变一下顺序，如改为0、6、3，就可以得到一个新终局。此外，4到6，7到9行也可以更改。于是一个数列可以生成$ 6^3=216 $个终局，由于第一位是固定的，所以只有八个数字8！= 40320个数列。

选取

​ 分性上述方法，回溯法生成的数独终局随机性非常高，但是效率相对较低，想要达到题目要求需要消耗大量时间和计算机资源；以宫为单位的矩阵置换法，通过矩阵行列变换有2!×3!×3!×2!×3!×3!=5184，要想生成1000000个终局，中间的九宫格就需要1000000/5184=192，而正中九宫格有8!=40320个足够满足要求，但由于需要控制多个九宫格进行矩阵变换，还是较为复杂；模板数字替换法效率较高，但是如果只使用一个模板的话，最多能生成的不同的数独终局数仅为9！=362880，而本项目中规定数独终局的第一行第一列为定值，使一个模板能生成的不同的数独终局数为8！=40320，显然是远远无法达到题目要求的数量上限（N<=1000000）。对于数列法，不仅高效，生成的终局数量达到目标要求，而且操作简单而快速，但终局相差不多。

​ 最终权衡，我决定使用方法四——数列法，来产生最终的数独终局。由于实验要求左上角的数字是(学号后两位相加)%9+1,所以生成数列时先固定好第一位数字，剩下的8位数字全排列8!也就是约为40000，是要求最大的终局数为1000000，所以最终一个排列需要1000000/40000 = 25，也就是每种排列需要生成25个终局。本实验中每种排列生成30个终局。

求解数独

方法

• 递归回溯法

  1. 如果全部填完，那么该数独的这种填法就是其中一种解，输出该数独解。
  2. 如果还没填完，填到了第x，y位置，判断该位置是否有数字（原题该位置有就有，没有就没有），如果有，填下一个位置。如果没有，寻找1-9数字在三个flag中为0的数字。找到了，标记flag（3个）为1，填下一个位置。
  3. 回溯法是恢复之前的flag和数据，即恢复为0，因此，每次填完数字，即在尝试该数据填完后，恢复flag和原来的数独数字

• 排除候选猜测法

  1. 传入数独矩阵，确定的数字直接填到对应的坐标上，没有填上数字的坐标可能候选值是1~9，再根据确定的值排除候选值。
  2. 当通过一般数独规则将候选值排除完，若答案仍不能确定，那么就开始进行点的猜测。
  3. 知道所有框中的数字都是确定的，就将其输出。

选取

• 最终综合考虑，当遇到困难级别的数独时，排除候选猜测法的效率是要高于递归回溯法。

  下列是我的测试结果：

  8 0 0 0 0 0 0 0 0
  0 0 3 6 0 0 0 0 0
  0 7 0 0 9 0 2 0 0
  0 5 0 0 0 7 0 0 0
  0 0 0 0 4 5 7 0 0
  0 0 0 1 0 0 0 3 0
  0 0 1 0 0 0 0 6 8
  0 0 8 5 0 0 0 1 0
  0 9 0 0 0 0 4 0 0
  
  排除候选测试法：0.0100 seconds
  递归回溯法：    0.1262 seconds

  最终决定选取排除候选测试法。

设计实现过程

模块介绍

主控模块

'''
根据参数调用下列函数进行相应处理（包括参数合法性判断）
'''

生成终局模块

• 数列法

1. 确定一个初始数列。
2. 由当前数列生成全排列中的一种。
3. 由上述得到的排列，按照之前所说原则进行移动操作，最终生成一个终局。
4. 检查生辰的终局数是否达到要求，如果没有达到，则返回第3步。

• 代码组织

'''
终局生成类：
移动变换元组、求解下一个全排列函数、初始化函数
'''

数独求解

• 代码组织

'''
数独求解类：
初始化函数、记录函数、检错函数、回溯函数、估值函数、排除侯选数函数、深度优先遍历
'''

思路流程图

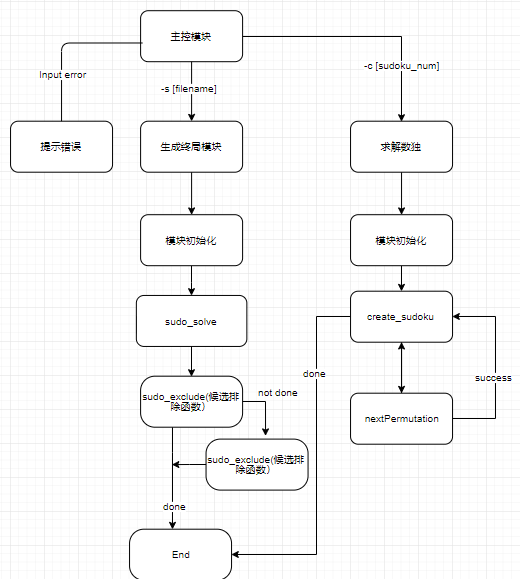
性能分析及优化

生成终局部分性能分析及优化

• 执行命令

  python3 sudoku.py -c 1000000

语言	生成1000000个终局所耗时间
python	30.9375
c/c++	2.460

• 模块时间分布

  使用【调试】中的启动python分析得到

  

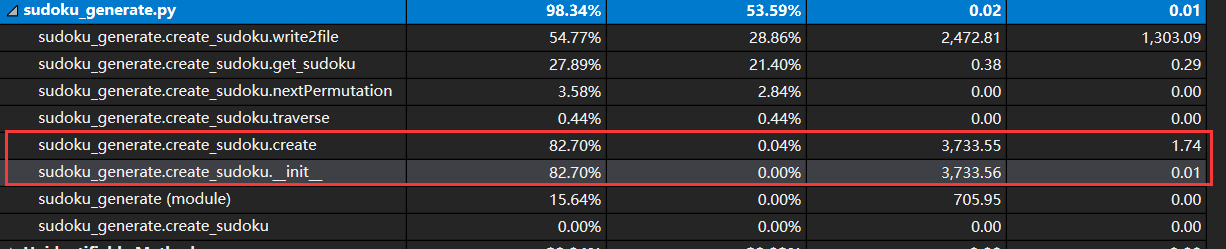
  由图中分析可以知道占用时间主要集中于__init__和create。

• 函数时间分布

  

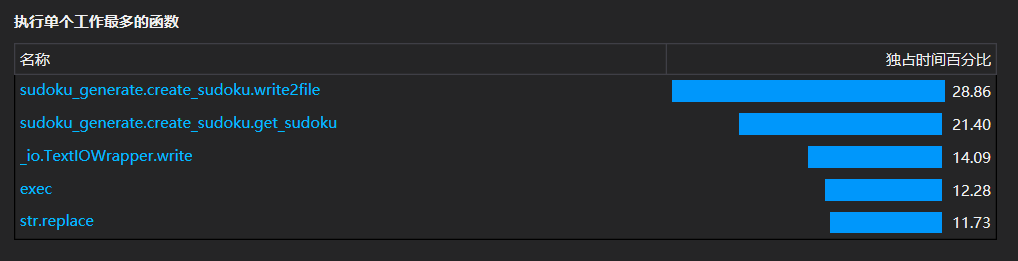
  时间消耗主要集中于write2file函数以及get_sudoku函数中。

• 时间分布图

  #为了能够更加直观的看出那个模块以及函数的时间消耗，增加了利用cprofile(分析时间）以及gprof2dot（可视化）
  #参考文献进行了性能分析: https://zhuanlan.zhihu.com/p/24495603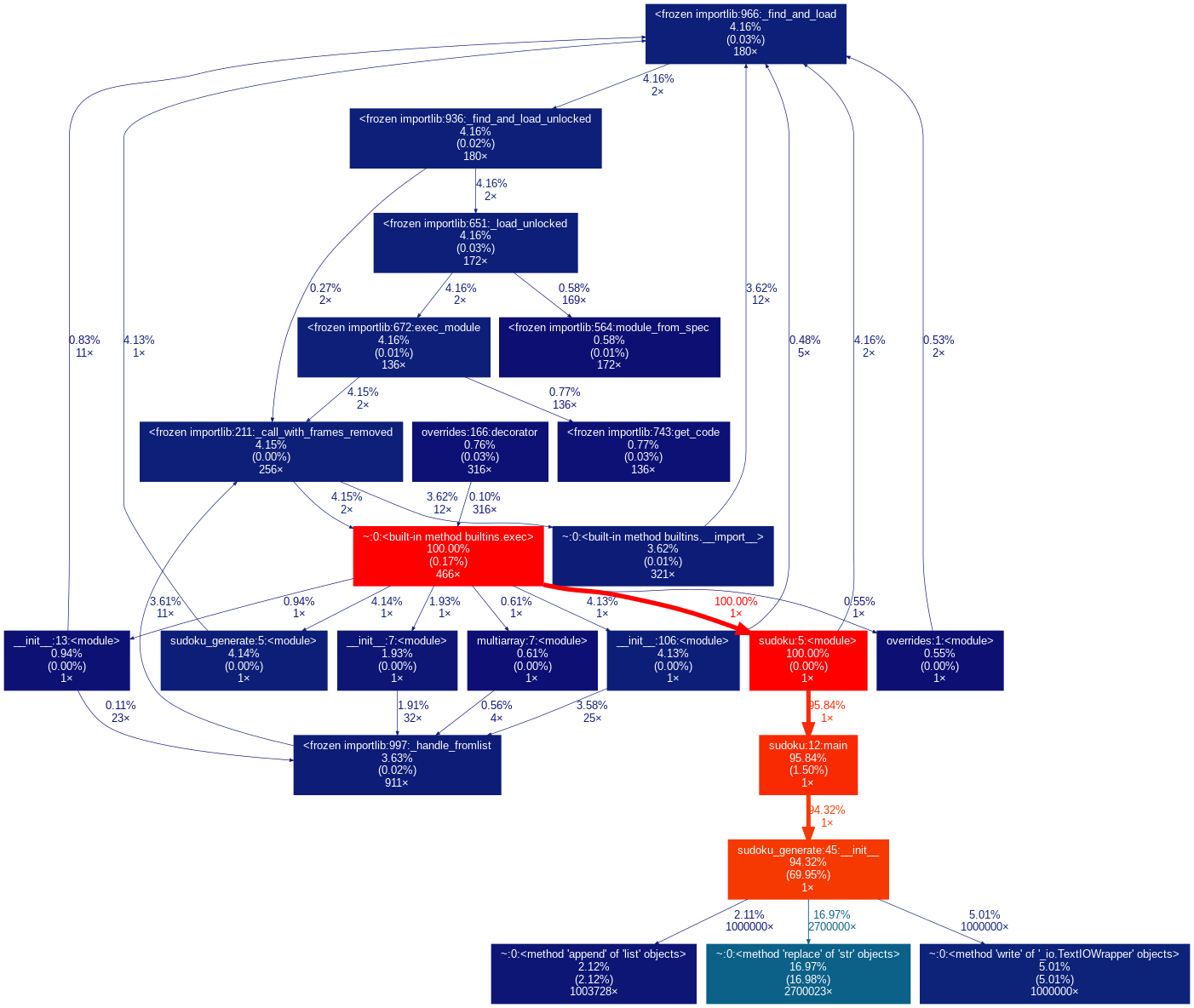

  

此处可以看出replace切割相对于其他比较耗时。

• 原因分析及解决方案

  ​ 首先是write2file以及get_sudoku函数，最开始的思路是得到一个终局写入一次，但事实证明效率极低，目前采用的策略是将全部的数独存到一个list变量perm中，最后集中写入。而replace比较耗时，这是因为python本身的特性决定的，python是一种解释性语言，前期的编译是将 Python 代码编译成解释器可以理解的中间代码，解释器再将中间代码翻译成CPU可以理解的指令,相比于 AOT(提前编译型语言，比如C)直接编译成机器码，肯定是慢的。那么要怎样才能使用python到达c的速度呢?由此我决定使用cython(一种C语言与python的结合体)写数独过程。学习过程参看博客。

  ​ 另外，生成全排列的函数nextPermutation，采取的措施是每次遍历完30个move_way之后才会获取下一个全排列，大大增加了该函数的调用次数，也浪费了时间。由此，我之后采用先将所有的全排列生成然后存储起来，之后直接访问即可。

  ​ 最后就是文件写入函数也会有占用大量时间，目前采用的策略是对于每一个数独，逐个写入，这样会多次调用write函数，所以最终的方案是建立一个缓存区，将数独以字符串形式存入，最后一起写入。结合cython，可以使用更快的fputs进行一次性写入。

• 最终结果

  #执行下列命令
  python3 sudoku.py -c 1000000

语言	生成1000000个数独终局所耗时间
python(最开始)	30.9375
c/c++	2.4605
cython	2.6758

解数独性能及优化

• 函数时间分布

  使用【调试】中的启动python分析得到

  

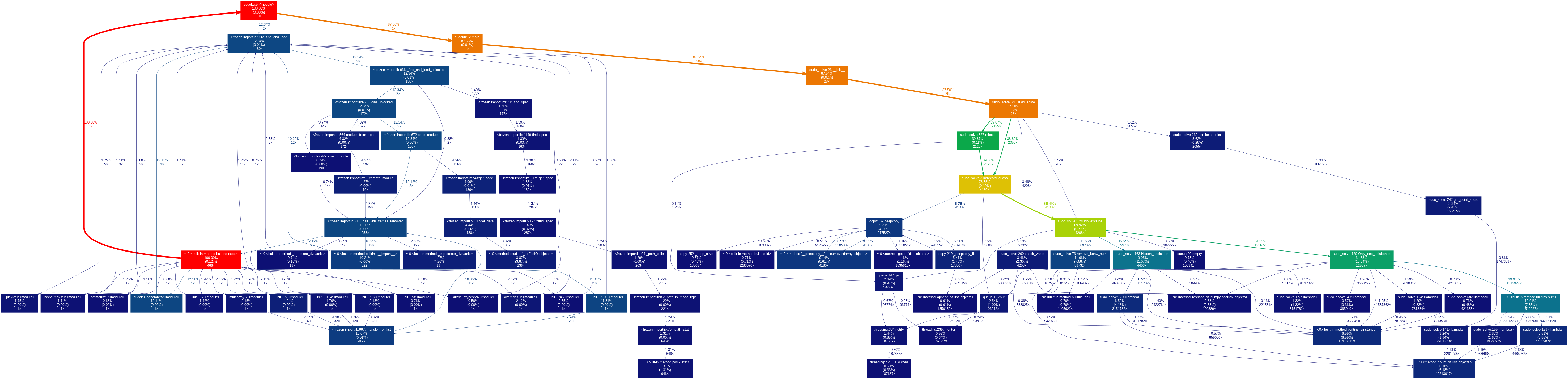
• 时间分布图

  

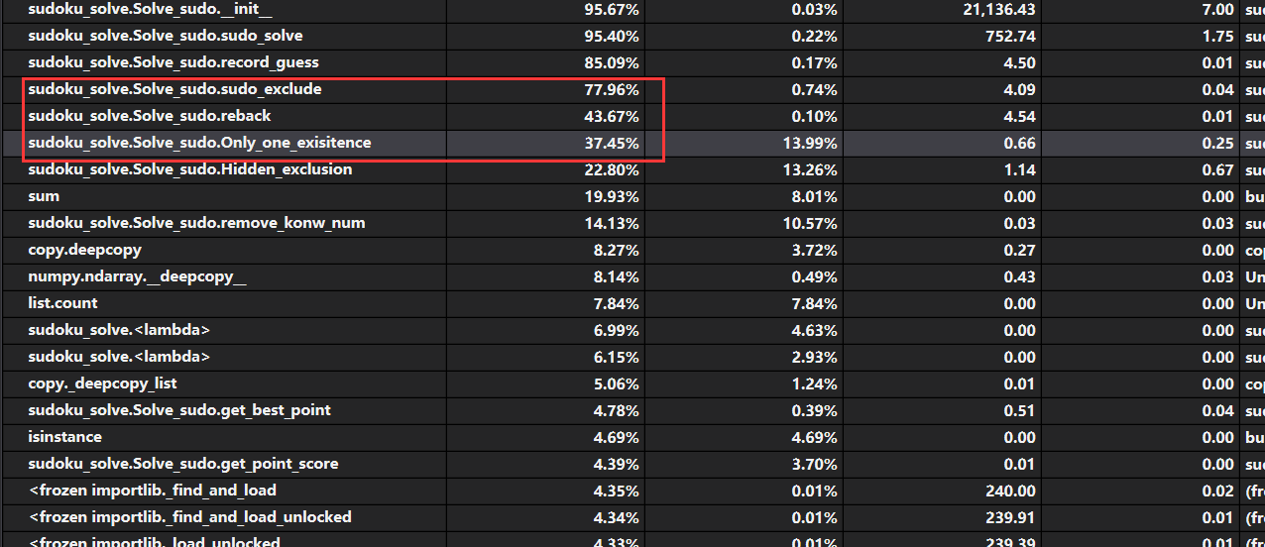
  从上面的图中可以看出来，guess函数耗时过多，其次就是排除候选的三种算法耗时也比较多。

• 原因分析

  • python语言本身的原因
  • 没有将其变为字符串一次写入，在write上耗时过多

• 解决方案

  • 建立一个缓冲区，优化写入过程
  • 优化一下排除候选的算法

单元测试以及覆盖率

单元测试

这里仅展示部分单元测试，具体可以去gihub仓库上进行相应查看。

对sudo_solve类下的remove_know_num进行的单元测试：

import unittest
from sudo_solve import Solve_sudo
from copy import deepcopy

'''
这是测试单元测试函数，将预计结果从ans.txt中提取出来，存入Ans中，
使用unittest进行单元测试，对结果进行比较 
'''
Ans = []
with open("ans.txt", 'r') as f:
    line = f.readline()
    cur_row = 0  #记录当前是否是第九行
    temp = []
    while line:
        if(line[0] != '\n' and cur_row != 9):
            line = [int(i) for i in line if str.isdigit(i)]
            temp.append(deepcopy(line))
            cur_row += 1
            line = f.readline()
        # 已经收集了一个数独
        elif cur_row == 9 or line[0] == '\n':
            line = f.readline()
            Ans.append(temp)
            cur_row = 0
            temp = []
    Ans.append(temp)

num = 0
class MyclassTest(unittest.TestCase):
    def setUp(self) -> None:
        self.sudoku = Solve_sudo(str(num)+".txt")

    def test_remove_konw_num(self):
        ret = self.sudoku.remove_konw_num()
        # print(ret)
        # print(Ans[num])
        self.assertEqual(ret,Ans[num]) 


def start():
    suite = unittest.TestSuite()
    suite.addTest(MyclassTest('test_remove_konw_num'))
    runner = unittest.TextTestRunner()
    runner.run(suite)

if __name__ == '__main__':
    for i in range(12):
        print(i)
        num = i
        start()

覆盖率

这里我使用coverage进行代码覆盖率查询(coverage用法可以自己去网上进行相关查询)。

• 生成终局

  • 在BIN目录下，执行下列命令：

    coverage run sudoku.py -c 10000

  • 这时会在当前目录下生成.coverage文件，使用下面命令进行查看

    coverage report -m   #查看详细信息

    

  • 生成网页详细信息图

    coverage html -d report1

    这会在当前界面下生成一个report1文件夹

    

    

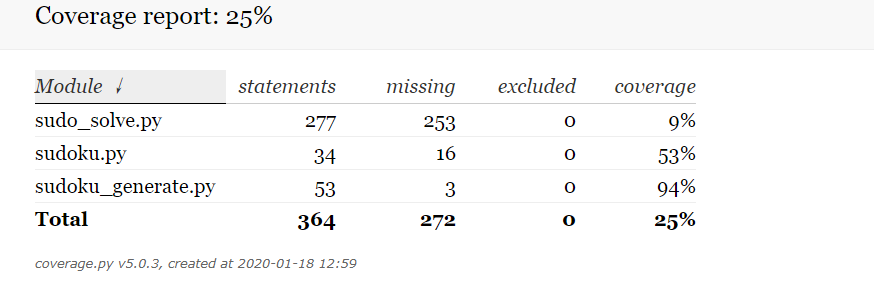
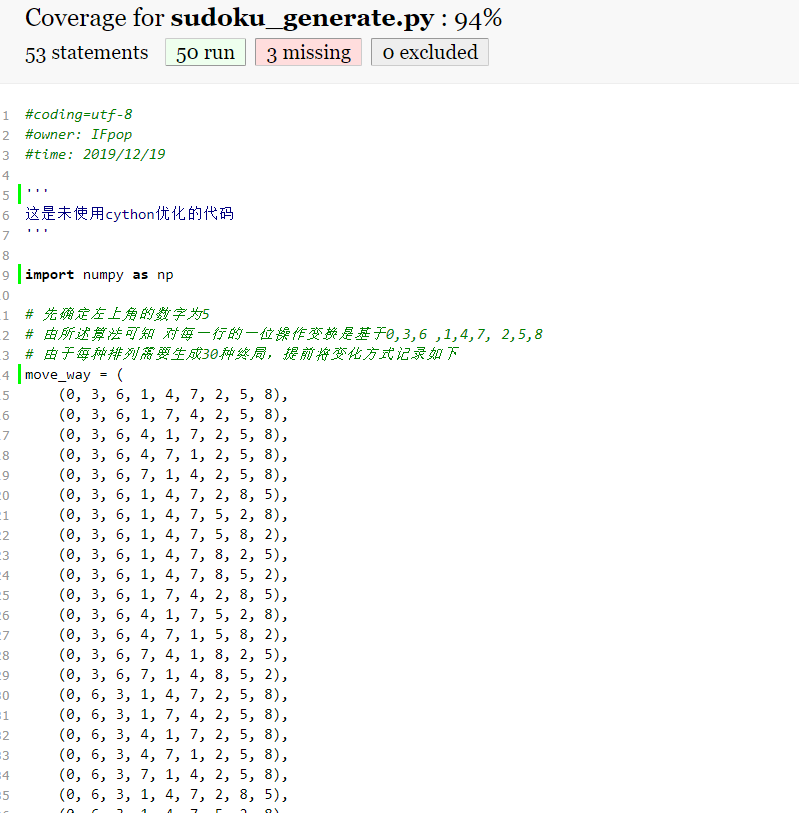
  由于此时调用的是sudoku_generate.py模块，所以该部分的覆盖率是94%，而对于sudoku.py而言通过指令占用的仅仅是一部分，仅有54%。所以代码冗余还算比较合理，出现bug的机率也比较小。

• 解数独

  • 同样，在BIN目录下，执行下列命令:

    coverage run sudoku.py -s test.txt

  • 对.coverage文件进行查看

    coverage report -m

    

  • 转成html进行查看

    coverage html -d report2

    这个命令会在当前目录下，生成一个report2文件夹，进入其中点击index进行查看

    

    

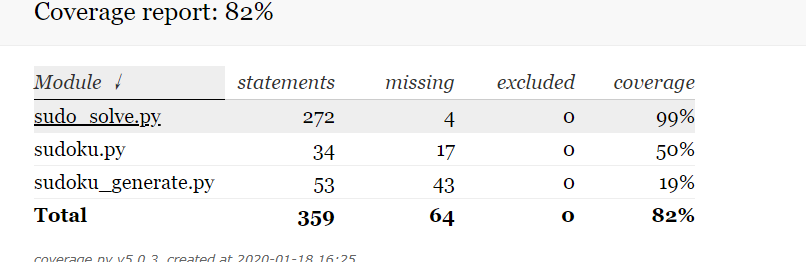
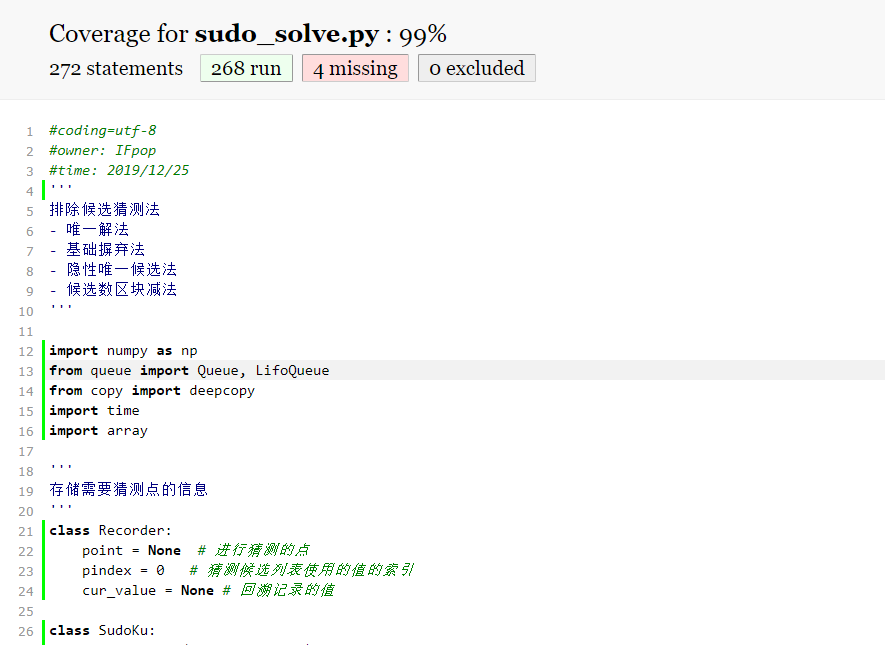
  此时只运行了sudo_solve部分，覆盖率达到99%，可见大部分的代码都被覆盖，bug出现几率也比较小。

代码说明

数独实现，使用类进行包装，并将其分为三个函数，下面对函数进行解释。

• 首先就是sudoku.py函数

  # sudoku.py
  
  #coding=utf-8
  #owner: IFpop
  #time: 2019/12/20
  
  # 生成终局模块
  import sudoku_generate
  # 解数独终局模块
  import sudo_solve
  from copy import deepcopy
  import sys
  import time
  
  def print_help():
      print("sudoku.exe [选项] 参数")
      print("选项：")
      print("    -c <数字>\t生成<数字>个数独终局至文件sudoku.txt")
      print("    -s <绝对路径>\t从<绝对路径>中读取数独题目并生成一个可行解至sudoku.txt")
      print("    -h 显示当前帮助信息")
  
  def main():
      # 判断参数是否是三个，那么此时就直接打印提示信息
      if len(sys.argv) != 3 or sys.argv[1] not in ['-c', '-s', '-h']:
          print_help()
      else:
          # 使用while，可以持续输入指令
          while 1:
              try:
                  cmd = sys.argv[1]
                  print("cmd:"+cmd)
                  # 如果是-c的话。就执行create
                  if cmd[1] == 'c':
                      # 确定开始时间
                      start = time.process_time()
                      num = int(sys.argv[2])
                      # 开始生成终局
                      sudoku_generate.create_sudoku(num)
                      # 确定结束时间
                      end = time.process_time()
                      print("running time is %6.4f" % (end-start))
                  elif cmd[1] == 's':
                      start = time.process_time()
                      # 第二个参数应该是数独文件路径
                      path = sys.argv[2]
                      sudo_solve.Solve_sudo(path)
                  elif cmd[1] == 'h':
                      print_help()
              except ValueError:
                  print("please input correct number")
  
  main()

  这是数独的主控函数，如果当前没有输入指令的话，那么使用print_help打印用法提示，将生成终局以及解数独包装成模块，使用模块接口进行调用。捕捉输入参数，会有三种情况，一种是输入指令python sudoku.py -c [你想生成的数量]，此时cmd = c，一种是输入指令python sudoku.py -s [想解的数独路径]，此时cmd = s，注意，这里路径既可以是绝对路径也可以是相对路径，最后一种是输入指令python sudoku.py -h，打印提示信息。关于报错信息，如果是值参数错误，那么就会爆出"please input correct number"。最后，使用系统time模块，打印函数执行所耗时间。

• 其次就是sudoku_generate.py，用于生成终局。

  # sudoku_generate.py
  #coding=utf-8
  #owner: IFpop
  #time: 2019/12/24
  
  import sys
  import time
  from libc.stdio cimport FILE, fopen, fclose, fputs, fgets, feof, fputc
  
  # 将移动顺序用元组存储起来，方便直接调用，加快速度
  move_way = (
      (0, 3, 6, 1, 4, 7, 2, 5, 8),
      (0, 3, 6, 1, 7, 4, 2, 5, 8),
      (0, 3, 6, 4, 1, 7, 2, 5, 8),
      (0, 3, 6, 4, 7, 1, 2, 5, 8),
      (0, 3, 6, 7, 1, 4, 2, 5, 8),
      (0, 3, 6, 1, 4, 7, 2, 8, 5),
      (0, 3, 6, 1, 4, 7, 5, 2, 8),
      (0, 3, 6, 1, 4, 7, 5, 8, 2),
      (0, 3, 6, 1, 4, 7, 8, 2, 5),
      (0, 3, 6, 1, 4, 7, 8, 5, 2),
      (0, 3, 6, 1, 7, 4, 2, 8, 5),
      (0, 3, 6, 4, 1, 7, 5, 2, 8),
      (0, 3, 6, 4, 7, 1, 5, 8, 2),
      (0, 3, 6, 7, 4, 1, 8, 2, 5),
      (0, 3, 6, 7, 1, 4, 8, 5, 2),
      (0, 6, 3, 1, 4, 7, 2, 5, 8),
      (0, 6, 3, 1, 7, 4, 2, 5, 8),
      (0, 6, 3, 4, 1, 7, 2, 5, 8),
      (0, 6, 3, 4, 7, 1, 2, 5, 8),
      (0, 6, 3, 7, 1, 4, 2, 5, 8),
      (0, 6, 3, 1, 4, 7, 2, 8, 5),
      (0, 6, 3, 1, 4, 7, 5, 2, 8),
      (0, 6, 3, 1, 4, 7, 5, 8, 2),
      (0, 6, 3, 1, 4, 7, 8, 2, 5),
      (0, 6, 3, 1, 4, 7, 8, 5, 2),
      (0, 6, 3, 1, 7, 4, 2, 8, 5),
      (0, 6, 3, 4, 1, 7, 5, 2, 8),
      (0, 6, 3, 4, 7, 1, 5, 8, 2),
      (0, 6, 3, 7, 4, 1, 8, 2, 5),
      (0, 6, 3, 7, 1, 4, 8, 5, 2),
  )
  
  cdef class create_sudoku:
      cdef FILE* Save_txt  #创建文件类型
      cdef list sudo_num,cur_first_row
      cdef list perm          #记录所有全排列 以5开头
      cdef int cur            #用于生成全排列
      cdef int index          #进行缓存区计数
      cdef char buf[1000200]  #创建缓存区
  
      def __init__(self,num:int):
          #打开文件句柄
          self.Save_txt = fopen('sudoku.txt', 'w+')
          if self.Save_txt == NULL:
              print("open failed!")
              sys.exit(0)
          
          # 生成初始的第一行1-9
          self.sudo_num = list(range(1, 10))
          # 将学号移动到前列
          self.sudo_num.remove(5)
          #记录当前第一行
          self.cur_first_row = [5]+self.sudo_num
          # 用于生成全排列
          self.cur = 1
          # 初始化全排列
          self.perm = []
  
          # 初始化缓存区
          self.index = 0
  
          #计时加运行
          cdef double start_time = time.time()
          self.create(num)
          cdef double end_time = time.time()
          print("running time: %.4f" % (end_time-start_time))
  
      '''
      将数独以字符串的形式写入缓存区
      '''
      cdef void write2buf(self,sudoku:list,n:int):
          cdef int i
          cdef int j
          if n != 0:
              self.buf[self.index] = 10 # '\n'
              self.index += 1
          for i in range(9):
              for j in range(9):
                  if j != 0:
                      self.buf[self.index] = 32  # ' '
                      self.index += 1
                  self.buf[self.index] = sudoku[i][j] + 48 # 0
                  self.index += 1
              self.buf[self.index] = 10
              self.index += 1
          #print(len(self.buf)) 
      
      '''
      根据第一行生成数独
      '''
      cdef get_sudoku(self,n:int,rows:list):
          # 临时变量存取数独
          cdef list Grid_sudoku = []
          num = n % 30
          for i in move_way[num]:
              Grid_sudoku.append(rows[-i:]+rows[:-i])
          return Grid_sudoku
      
      '''
      递归计算出所有全排列结果
      '''
      cdef permutation(self,list a_row):
          cdef list temp
          if not a_row:
              self.perm.append(list(self.cur_first_row))
              return
          for i in a_row:
              self.cur_first_row[self.cur] = i
              self.cur += 1
              temp = list(a_row)
              temp.remove(i)
              self.permutation(temp)
              self.cur -= 1
      '''
      主控函数
      '''
      cdef create(self,num:int):
          cdef int i
          cdef int tag  #当前全排列
          # 生成所有全排列
          self.permutation(self.sudo_num)
          # 0~num-1
          for i in range(num-1):
              tag = i % 40320 
              # 将数独生成后，写入缓存区
              self.write2buf(self.get_sudoku(i,self.perm[tag]),i)
              # 缓存区已满，输入，然后初始化
              if self.index > 1000000:
                  self.buf[self.index] = 0
                  fputs(self.buf,self.Save_txt)
                  self.index = 0
          tag = num % 40320
          self.write2buf(self.get_sudoku(i,self.perm[tag]), num)
          fputs(self.buf, self.Save_txt)
          fclose(self.Save_txt)

  该代码使用cython编写，建立一个字符串，最后一次性写入文件。将所有的排列先全部算出来，存入self.perm之中，方便更加快速调用。

• sudo_solve.py函数，用于求解数独。

  由于这部分比较复杂，就分函数进行解释。

  • 首先就是Recorder类

    '''
    存储需要猜测点的信息
    '''
    class Recorder:
        point = None  # 进行猜测的点
        pindex = 0   # 猜测候选列表使用的值的索引
        cur_value = None # 回溯记录的值

  • SudoKu类，用于存储求解数独的必要信息

    class SudoKu:
        def __init__(self,data:list)->None:
            self.sudoku = np.array(data) #数据初始化
            self.value =np.array([[0] * 9] * 9, dtype=object) #当前数独初始化
            self.runtime = 0 #初始化运行时间
            self.know_points = Queue() #先进先出，新解(已解决值)的点对
            self.recorder = LifoQueue() #先进后出，回溯器
            self.guess_times = 0
    
             # 对数独进行处理
            for row in range(9):
                for col in range(9):
                    if self.sudoku[row][col]:  # 如果是已确定点
                        self.value[row][col] = int(self.sudoku[row][col])
                        # 新的确认的值添加到列表中，以便遍历
                        self.know_points.put((row, col))
                    else:
                        self.value[row][col] = [1, 2, 3, 4, 5, 6, 7, 8, 9]

  • 最后就是解数独类Solve_sudo

    这部分函数代码量较大，想知详情，可去github仓库进行查看，这里仅对关键函数进行说明。

    • 递归求解,sudo_solve函数。

      这是求解数独的主控函数。

      def sudo_solve(self):
             #第一次解题，排除法
             self.sudo_exclude()
             #检查有没有错误，有错误则回溯，没错误却未解开题目，则再猜测
             while True:
                 if(self.check_value()):
                     fixed_answer = 0
                     for i in self.current_sudoku.value.reshape(1, -1)[0]:
                         if(isinstance(i,int)):
                             fixed_answer += 1
                     if(fixed_answer == 81):
                         break
                     else:
                         #获取最佳猜测点
                         point = self.get_best_point()
                         self.record_guess(point)
                 else:
                     self.reback()

    • 使用基础摒弃法，排除隐含值。

      基础摒弃法是利用已知的值，去除隐含的值

      def remove_konw_num(self, point):
              # 获取该点的横纵列坐标
              row, col = point
              # 通过坐标获取对应值
              val = self.current_sudoku.value[row, col]
      
              # 检查行
              for i, item in enumerate(self.current_sudoku.value[row]):
                  if(isinstance(item, list)):
                      # 统计该点在该行出现的次数
                      if(item.count(val)):
                          item.remove(val)  # 移除
                          # 判断移除后，是否剩下一个元素
                          if(len(item) == 1):
                              self.current_sudoku.know_points.put((row, i))  # 添加该坐标到已解决
                              self.current_sudoku.value[row][i] = item[0]
              # 检查列
              for i, item in enumerate(self.current_sudoku.value[:, col]):
                  if isinstance(item, list):
                      if item.count(val):
                          item.remove(val)
      
                          # 判断移除后，是否剩下一个元素
                          if len(item) == 1:
                              self.current_sudoku.know_points.put((i, col))
                              self.current_sudoku.value[i][col] = item[0]
              # 检查九宫格
              # 先找到九宫格基准点，也就是3×3数组的左上角的点
              bp_row, bp_col = map(lambda x: x // 3 * 3, point)
              # print(bp_row, bp_col)
              # 在3×3的矩阵里进行排除
              for m_r, row in enumerate(self.current_sudoku.value[bp_row:bp_row + 3, bp_col:bp_col + 3]):
                  for m_c, item in enumerate(row):
                      if(isinstance(item, list)):
                          if(item.count(val)):
                              item.remove(val)
      
                              # 判断移除后
                              if len(item) == 1:
                                  r = bp_row + m_r
                                  c = bp_col + m_c
                                  self.current_sudoku.know_points.put((r, c))
                                  self.current_sudoku.value[r][c] = item[0]

    • 使用唯一解法排除候选

      如果一行、一列、九宫格仅剩余一空未填，那么就直接填入剩余值

      '''
          For a class that can directly determine other rows, columns or nine palace cells, the point can be directly determined
          '''
          def Only_one_exisitence(self):
              # 同一行只有一个数字的情况
              for row in range(9):
                  # 只取出的是这一行是list格子
                  vals = list(filter(lambda x: isinstance(x, list), self.current_sudoku.value[row]))
                  # print(val) #得到该行的所有可能性的二维数组
                  for col, item in enumerate(self.current_sudoku.value[row]):
                      if(isinstance(item, list)):
                          for value in item:  # 对其中的每个元素判断，如果只出现一次则确定
                              if(sum(map(lambda x: x.count(value), vals)) == 1):
                                  self.current_sudoku.value[row][col] = value
                                  self.current_sudoku.know_points.put((row, col))
                                  return True
              # 对于列
              for col in range(0, 9):
                  vals = list(
                      filter(lambda x: isinstance(x, list), self.current_sudoku.value[:, col]))
      
                  for row, item in enumerate(self.current_sudoku.value[:, col]):
                      if(isinstance(item, list)):
                          for value in item:
                              if(sum(map(lambda x: x.count(value), vals)) == 1):
                                  self.current_sudoku.value[row][col] = value
                                  self.current_sudoku.know_points.put((row, col))
                                  return True
      
              # 对于九宫格
              for row, col in self.base_points:
                  # reshape: 3x3 改为1维数组
                  vals = list(filter(lambda x: isinstance(x, list),
                                     self.current_sudoku.value[row:row + 3, col:col + 3].reshape(1, -1)[0]))
                  for m_r, rows in enumerate(self.current_sudoku.value[row:row + 3, col:col + 3]):
                      for m_c, item in enumerate(rows):
                          if(isinstance(item, list)):
                              for value in item:
                                  if(sum(map(lambda x: x.count(value), vals)) == 1):
                                      self.current_sudoku.value[row + m_r, col + m_c] = value
                                      self.current_sudoku.know_points.put((row + m_r, col + m_c))
                                      return True

    • 使用候选数区块删减法排除候选

      1. 在某一九宫格中，当所有可能出现某个数字的单元格都位于同一行时，就可以把这个数字从该行的其他单元格的候选数中删除；
      2. 在某一九宫格中，当所有可能出现某个数字的单元格都位于同一列时，就可以把这个数字从该列的其他单元格的候选数中删除；
      3. 在某一行（列）中，当所有可能出现某个数字的单元格都位于同一九宫格中时，就可以把这个数字从该九宫格的其他单元格的候选数中删除。。

      '''
         Invisible elimination of the same row in the nine palace grid
         '''
         def Hidden_exclusion(self):
             for bp_r, bp_c in self.base_points:
                 block = self.current_sudoku.value[bp_r:bp_r + 3, bp_c:bp_c + 3]
            
                 # 判断数字1~9在该九宫格的分布情况,reshape变为一维
                 _data = block.reshape(1, -1)[0]
                 for i in range(1, 10):
                     result = map(lambda x: 0 if not isinstance(x[1], list) else x[0] + 1 if x[1].count(i) else 0,
                                  enumerate(_data))
                     result = list(filter(lambda x: x > 0, result))
                     r_count = len(result)
            
                     if r_count in [2, 3]:
                         # 2或3个元素才有可能同一行或同一列
                         rows = list(map(lambda x: (x - 1) // 3, result))
                         cols = list(map(lambda x: (x - 1) % 3, result))
            
                         if len(set(rows)) == 1:
                             # 同一行，去掉其他行的数字
                             result = list(
                                 map(lambda x: bp_c + (x - 1) % 3, result))
                             row = bp_r + rows[0]
            
                             for col in range(0, 9):
                                 if not col in result:
                                     item = self.current_sudoku.value[row, col]
                                     if isinstance(item, list):
                                         if item.count(i):
                                             item.remove(i)
            
                                             # 判断移除后，是否剩下一个元素
                                             if len(item) == 1:
                                                 self.current_sudoku.know_points.put((row, col))
                                                 self.current_sudoku.value[row, col] = item[0]
                                                 return True
                         elif len(set(cols)) == 1:
                             # 同一列
                             result = list(
                                 map(lambda x: bp_r + (x - 1) // 3, result))
                             col = bp_c + cols[0]
            
                             for row in range(0, 9):
                                 if not row in result:
                                     item = self.current_sudoku.value[row, col]
                                     if isinstance(item, list):
                                         if item.count(i):
                                             item.remove(i)
            
                                             # 判断移除后，是否剩下一个元素
                                             if len(item) == 1:
                                                 self.current_sudoku.know_points.put((row, col))
                                                 self.current_sudoku.value[row, col] = item[0]
                                                 return True

界面设计

界面思路

1. 可以动态显示当前时间，年月日
2. 可以选择难度Level，分为Easy、Medium、Hard
3. 可以显示当前所选难度
4. 可以显示剩余的空格数量，并在数独界面上将空格置为绿色(便于观察)
5. 设有start的按钮，用于游戏开始以及重开
6. 设有next，代表下一步，也代表提示功能，当点击下一步时，可以帮你随机填入一个点
7. 设有last，代表上一步，可以恢复上一状态
8. 设置图片，标识此前状态，有未开始游戏，开始游戏，游戏失败，游戏成功
9. 对于每一个输入，都要对其进行判断
   • 如果是行发生问题，将此格标红
   • 如果是列发生问题，将此格标红
   • 如果是九宫格发生问题，将此格标红
   • 否则，就正确进行下一步

界面实现效果

• 初始界面

  初始界面，尚未开始游戏，一切都是初始状态

  

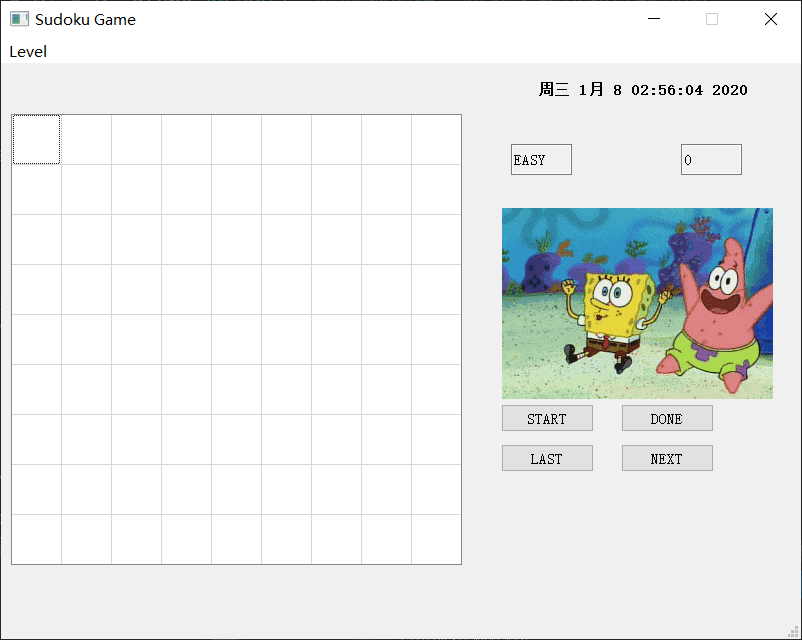
• 开始游戏

  点击start后，start按钮会变为restart，然后图片发现改变，右上角显示是空格个数，右边左上角显示的是难度。

  

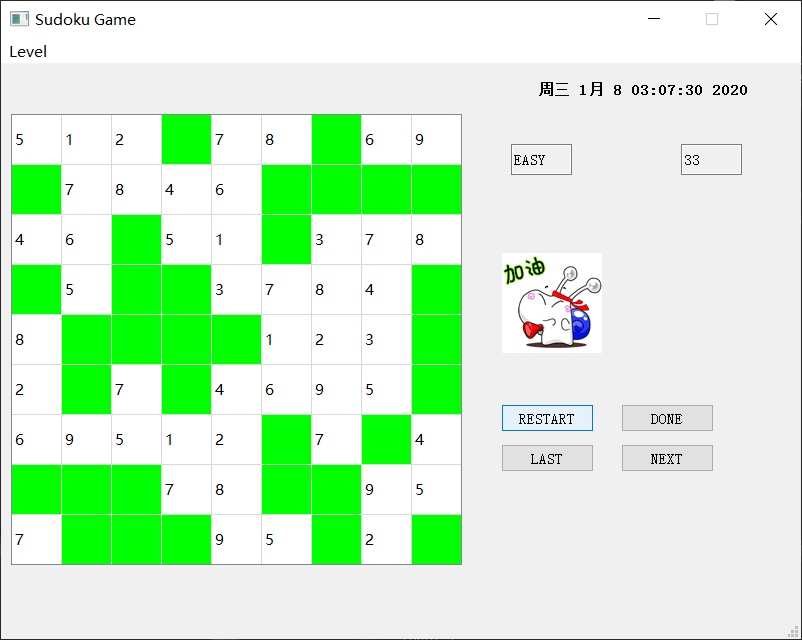
• 点击下一步进行补全

  如果点击 Next按钮，那么会帮助你随机填入当前一步。

  

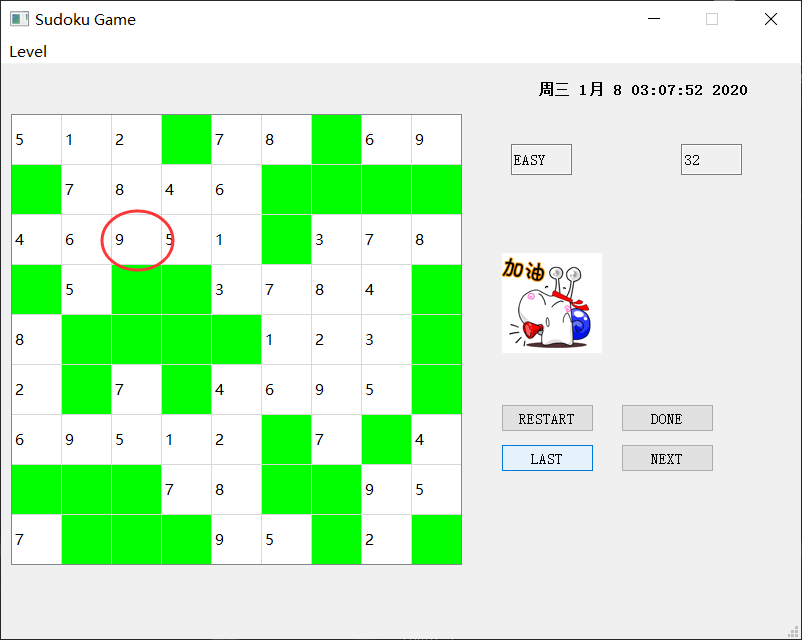
• 使用上一步进行恢复

  如果点击Last按钮，那么会撤回之前所走的一步。

  

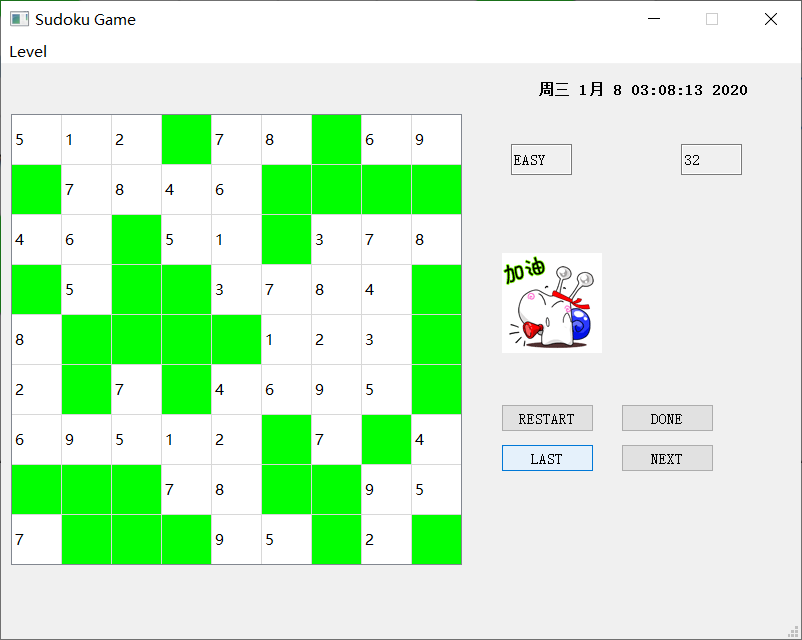
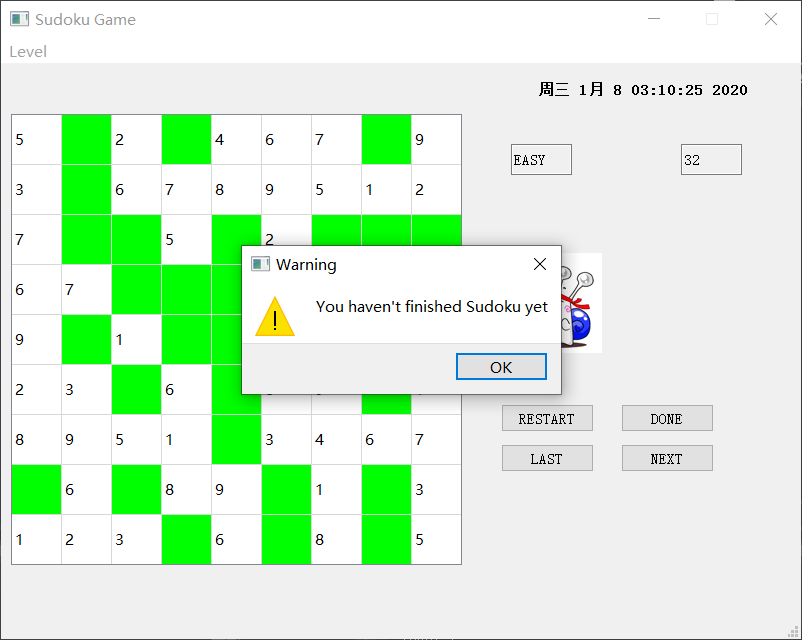
• 在未完成的情况下，点击DONE

  此时，会爆出提示未完成游戏的提示信息。

  

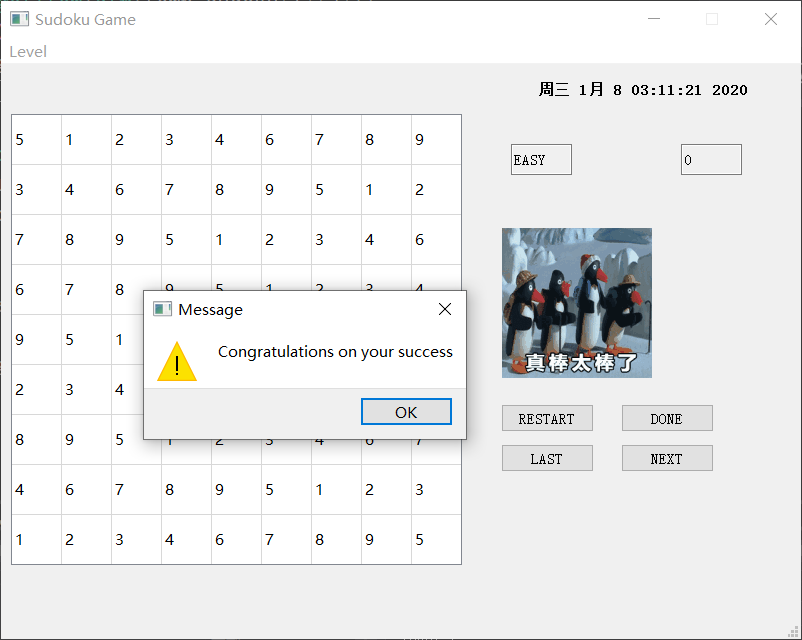
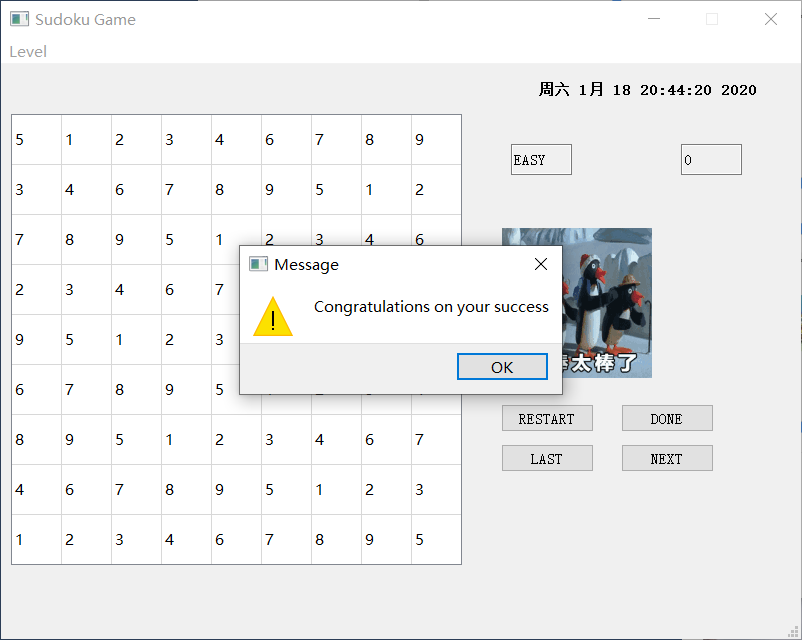
• 完成一局游戏后，如果正确，将会出现如下结果

  

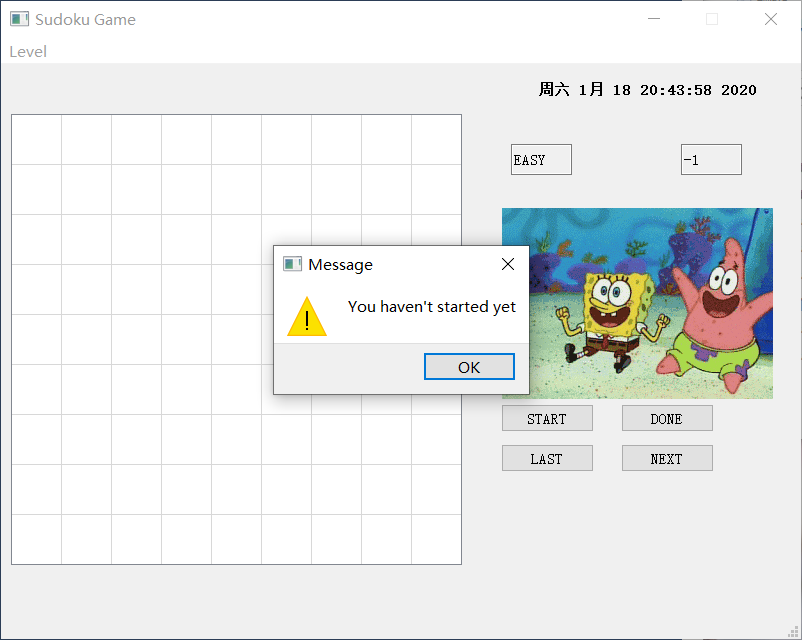
• 对于一些特殊情况的处理

  由于NEXT以及LAST是通过栈实现的，所以我对其边界进行了判断，如果在没有开始游戏的时候点击LAST,它会提示您尚未开始游戏，如下：

  

  如果点击NEXT一直到最后一步，那么就是执行Done的功能，具体效果如下：

  

感想

​ 这次数独项目开发，让我从零开始了解了软件开发的全过程，从需求分析到软件测试，对软件开发模型也有了一定的了解。其次就是学到了很多关于python项目编程的方法，以及对其进行处理的工具，如cython、pyqt、pyinstaller等等。对python编程的熟练度也得到了提高，特别是界面的编写，当然也有着很强的工具Qtdesign辅助编程。这次开发，也同时锻炼了思维以及寻找解决问题的能力，从刚开始对其完全不太了解到明白如何去做，这个过程是让我收获巨大的。

​ 老师的基本要求虽然已经实现，但还是有些地方不太完善，如单元测试部分，我发现有些类中的函数并不是很容易能进行单元测试，需要和其他函数一起，才能测试其中内容，这也可能是模块独立性还是不高导致的。

​ 总而言之，这次开发让我收获颇多，以后也必会越来越熟练。

​